1. 在 $\triangle ABC$ 中,$AB = 15$,$AC = 13$,高线 $AD = 12$,则 $\triangle ABC$ 的周长是
42或32
。
答案:
42或32
2. 如图,在直线 $l$ 上依次摆放着七个正方形,已知斜放置的三个正方形的面积分别是 $1$,$2$,$3$,正放置的四个正方形的面积依次是 $S_{1}$,$S_{2}$,$S_{3}$,$S_{4}$,则 $S_{2} + S_{3} = $

2
,$S_{1} + S_{4} = $2
。
答案:
2 2
3. 已知等腰直角三角形 $ABC$ 的两条直角边 $AB = AC = 10$,以 $AB$ 为边在 $\triangle ABC$ 的外面作等腰直角三角形 $ABD$,连结 $CD$,则 $CD$ 的长为
$ 5\sqrt{10} $,$ 10\sqrt{5} $,20
。
答案:
$ 5\sqrt{10} $,$ 10\sqrt{5} $,20
4. 如图,将长方形纸片 $ABCD$ 沿对角线 $AC$ 折叠,使点 $B$ 落在点 $E$ 处,$AB = 4$,$BC = 8$。
(1) 试判断折叠后重叠部分 $\triangle AFC$ 的形状。
小贴士:折叠后有很多边的长度、角的大小都是不变的,你发现了吗?
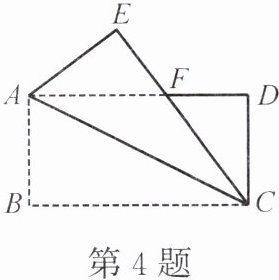
(2) 求重叠部分 $\triangle AFC$ 的面积。
(1) 试判断折叠后重叠部分 $\triangle AFC$ 的形状。
小贴士:折叠后有很多边的长度、角的大小都是不变的,你发现了吗?

(2) 求重叠部分 $\triangle AFC$ 的面积。
答案:
(1)等腰三角形 (2)10
5. 如图,等边三角形 $ABC$ 的边长为 6,$AD$ 是边 $BC$ 上的中线,$M$ 是 $AD$ 上的一动点,$E$ 是边 $AC$ 上的一点。若 $AE = 2$,则 $EM + CM$ 的最小值是多少?


答案:
$ 2\sqrt{7} $
查看更多完整答案,请扫码查看


