《2025年预学与导学八年级数学上册浙教版》

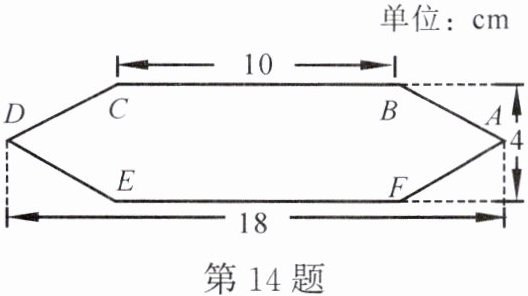
14. 如图,六边形$ABCDEF$是轴对称图形,且有两条对称轴,点$B的对称点既可以是点C$,也可以是点$F$。根据图中的数据,请你直接在图上建立一个平面直角坐标系,并写出点$A$,$B$,$C$,$D$,$E$,$F$的坐标。

答案： (答案不唯一)如:以E为原点,EF所在直线为x轴,1cm为一个单位长度,建立平面直角坐标系 则A(14,2),B(10,4),C(0,4),D(-4,2),E(0,0),F(10,0)

15. 已知点$P(2m+6,m+1)$,请分别根据下列条件,求出点$P$的坐标。
(1) 点$P在x$轴上。
(2) 点$P$的纵坐标比横坐标大1。
(3) 点$P在过点A(-4,2)且与y$轴平行的直线上。
(4) 点$P$在第四象限,且$m$是整数。

答案： $(1)$ 点$P$在$x$轴上
- **分析**：
在$x$轴上的点纵坐标为$0$，即$m + 1 = 0$。
- **求解**：
解$m + 1 = 0$，得$m=-1$。
将$m = - 1$代入横坐标$2m + 6$中，$2×(-1)+6=-2 + 6 = 4$。
所以点$P$的坐标为$(4,0)$。
$(2)$ 点$P$的纵坐标比横坐标大$1$
- **分析**：
根据纵坐标比横坐标大$1$，可列方程$(m + 1)-(2m + 6)=1$。
- **求解**：
解$(m + 1)-(2m + 6)=1$，
去括号得$m + 1-2m - 6 = 1$，
移项得$m-2m=1 + 6 - 1$，
合并同类项得$-m = 6$，
解得$m=-6$。
将$m = - 6$代入横坐标$2m + 6$中，$2×(-6)+6=-12 + 6=-6$；
代入纵坐标$m + 1$中，$-6 + 1=-5$。
所以点$P$的坐标为$(-6,-5)$。
$(3)$ 点$P$在过点$A(-4,2)$且与$y$轴平行的直线上
- **分析**：
与$y$轴平行的直线上的点横坐标都相等，所以$2m + 6=-4$。
- **求解**：
解$2m + 6=-4$，
移项得$2m=-4 - 6$，
合并同类项得$2m=-10$，
解得$m=-5$。
将$m = - 5$代入纵坐标$m + 1$中，$-5 + 1=-4$。
所以点$P$的坐标为$(-4,-4)$。
$(4)$ 点$P$在第四象限，且$m$是整数
- **分析**：
第四象限的点横坐标大于$0$，纵坐标小于$0$，即$\begin{cases}2m + 6\gt0\\m + 1\lt0\end{cases}$。
- **求解**：
解不等式$2m + 6\gt0$，
移项得$2m\gt - 6$，
解得$m\gt - 3$；
解不等式$m + 1\lt0$，
解得$m\lt - 1$。
所以$-3\lt m\lt - 1$，又因为$m$是整数，所以$m=-2$。
将$m = - 2$代入横坐标$2m + 6$中，$2×(-2)+6=-4 + 6 = 2$；
代入纵坐标$m + 1$中，$-2 + 1=-1$。
所以点$P$的坐标为$(2,-1)$。
综上，答案依次为：$(1)(4,0)$；$(2)(-6,-5)$；$(3)(-4,-4)$；$(4)(2,-1)$。

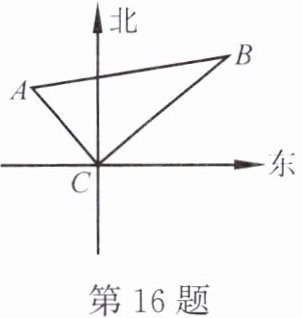
16. 如图,从上午9时到下午1时,轮船从$A处沿直线航行到B$处。在$A处测得灯塔在轮船南偏东40^{\circ}$方向20海里处,在$B处测得灯塔在轮船南偏西50^{\circ}方向20\sqrt{3}$海里处,求轮船航行的平均速度。

答案： 10海里/时

17. 在平面直角坐标系中,已知$O$为原点,点$A(0,2)$,$B(-2,0)$,$C(4,0)$。

(1) 如图①,$\triangle ABC$的面积为6。
(2) 如图②,将点$B$向右平移7个单位长度,再向上平移4个单位长度,得到点$D$。
①求$\triangle ACD$的面积。
②$P(m,3)$是一个动点,若$\triangle PAO的面积等于\triangle CAO$面积的2倍,请直接写出点$P$的坐标。
①9；②(8,3)或(-8,3)

答案： 1. （1）
已知$A(0,2)$，$B(-2,0)$，$C(4,0)$。
根据三角形面积公式$S = \frac{1}{2}×底×高$，在$\triangle ABC$中，以$BC$为底，$BC=\vert - 2 - 4\vert=6$，$A$到$x$轴的距离（即高）$h = 2$。
则$S_{\triangle ABC}=\frac{1}{2}× BC×2=\frac{1}{2}×6×2 = 6$。
2. （2）①
因为点$B(-2,0)$向右平移$7$个单位长度，再向上平移$4$个单位长度得到点$D$，根据平移规律“右加左减，上加下减”，则$D$点坐标为$(-2 + 7,0 + 4)$，即$D(5,4)$。
已知$A(0,2)$，$C(4,0)$，$D(5,4)$。
$S_{\triangle ACD}=S_{梯形AODC}-S_{\triangle AOC}-S_{\triangle ODD}$。
梯形面积公式$S_{梯形}=\frac{(a + b)h}{2}$（$a$、$b$为上、下底，$h$为高），$S_{梯形AODC}=\frac{(2 + 4)×5}{2}=15$；$S_{\triangle AOC}=\frac{1}{2}×4×2 = 4$；$S_{\triangle ODD}=\frac{1}{2}×(5 - 4)×4 = 2$。
所以$S_{\triangle ACD}=15-4 - 2=9$。
3. （2）②
已知$A(0,2)$，$O(0,0)$，$C(4,0)$，则$S_{\triangle CAO}=\frac{1}{2}×4×2 = 4$。
因为$S_{\triangle PAO}=2S_{\triangle CAO}$，所以$S_{\triangle PAO}=8$。
又因为$S_{\triangle PAO}=\frac{1}{2}× OA×\vert m\vert$，$OA = 2$，则$\frac{1}{2}×2×\vert m\vert=8$。
即$\vert m\vert = 8$，解得$m=\pm8$。
所以$P$点坐标为$(8,3)$或$(-8,3)$。
综上，答案依次为：（1）$6$；（2）①$9$；②$(8,3)$或$(-8,3)$。