1. 如图,AB = A'B',∠A = ∠A'。要使△ABC ≌ △A'B'C',需添加一个条件,添法有(

A.1种
B.2种
C.3种
D.4种
C
)。
A.1种
B.2种
C.3种
D.4种
答案:
C
2. 如图,点P在∠AOB的平分线上,不添加辅助线,要使△AOP ≌ △BOP,根据“SAS”,需添加的一个条件是

OA=OB
;根据“ASA”,需添加的一个条件是∠APO=∠BPO
;根据“AAS”,需添加的一个条件是∠OAP=∠OBP
。
答案:
OA=OB ∠APO=∠BPO ∠APO=∠BPB或∠OAP=∠OBP
3. 如图,在△ABC中,∠B = ∠C,点D,E,F分别在AB,BC,AC上,且BD = CE,∠DEF = ∠B。求证:ED = EF。(填空)
证明:
因为∠DEC = ∠B + ∠BDE(
∠DEC = ∠DEF + ∠FEC,
∠DEF = ∠B(已知),
所以∠
在△EBD与△FCE中,
因为{∠
∠B = ∠C(已知),
所以△EBD ≌ △FCE(
所以ED = FE(

证明:
因为∠DEC = ∠B + ∠BDE(
三角形的外角等于与它不相邻的两个内角和或三角形外角的性质
),∠DEC = ∠DEF + ∠FEC,
∠DEF = ∠B(已知),
所以∠
BDE
= ∠FEC
(等式性质)。在△EBD与△FCE中,
因为{∠
BDE
= ∠FEC
(已证),BD
= CE
(已知),∠B = ∠C(已知),
所以△EBD ≌ △FCE(
ASA
)。所以ED = FE(
全等三角形的对应边相等
)。
答案:
三角形的外角等于与它不相邻的两个内角和或三角形外角的性质 BDE FEC BDE FEC BD CE ASA 全等三角形的对应边相等
4. 如图,∠BAD = ∠CAE,∠B = ∠D,且AC = AE。求证:AB = AD。


答案:
提示:利用“AAS”证△ABC≌△ADE
5. 如图,已知AE = CF,AD // BC,DE ⊥ AC于点E,BF ⊥ AC于点F。
(1) 求证:DE = BF。
(2) 连结DF,BE,猜想DF与BE之间的数量关系和位置关系,并给予证明。
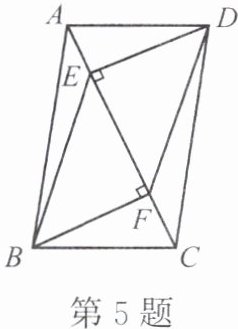
(1) 求证:DE = BF。
(2) 连结DF,BE,猜想DF与BE之间的数量关系和位置关系,并给予证明。

答案:
1. (1)证明:
因为$AD// BC$,所以$\angle DAE=\angle BCF$。
又因为$DE\perp AC$,$BF\perp AC$,所以$\angle AED = \angle CFB=90^{\circ}$。
已知$AE = CF$。
在$\triangle ADE$和$\triangle CBF$中:
$\begin{cases}\angle DAE=\angle BCF\\\angle AED=\angle CFB\\AE = CF\end{cases}$
根据$AAS$(两角及其中一角的对边对应相等的两个三角形全等),可得$\triangle ADE\cong\triangle CBF$。
由全等三角形的对应边相等,所以$DE = BF$。
2. (2)猜想:$DF = BE$且$DF// BE$。
证明:
因为$AE = CF$,所以$AE + EF=CF + EF$,即$AF = CE$。
又因为$\angle AFB=\angle CED = 90^{\circ}$,$BF = DE$(已证)。
在$\triangle ABF$和$\triangle CDE$中:
$\begin{cases}AF = CE\\\angle AFB=\angle CED\\BF = DE\end{cases}$
根据$SAS$(两边及其夹角对应相等的两个三角形全等),可得$\triangle ABF\cong\triangle CDE$。
所以$AB = CD$,$\angle BAF=\angle DCE$,则$AB// CD$。
所以四边形$BEDF$是平行四边形(一组对边平行且相等的四边形是平行四边形)。
所以$DF = BE$且$DF// BE$。
综上,(1)得证$DE = BF$;(2)$DF = BE$且$DF// BE$。
因为$AD// BC$,所以$\angle DAE=\angle BCF$。
又因为$DE\perp AC$,$BF\perp AC$,所以$\angle AED = \angle CFB=90^{\circ}$。
已知$AE = CF$。
在$\triangle ADE$和$\triangle CBF$中:
$\begin{cases}\angle DAE=\angle BCF\\\angle AED=\angle CFB\\AE = CF\end{cases}$
根据$AAS$(两角及其中一角的对边对应相等的两个三角形全等),可得$\triangle ADE\cong\triangle CBF$。
由全等三角形的对应边相等,所以$DE = BF$。
2. (2)猜想:$DF = BE$且$DF// BE$。
证明:
因为$AE = CF$,所以$AE + EF=CF + EF$,即$AF = CE$。
又因为$\angle AFB=\angle CED = 90^{\circ}$,$BF = DE$(已证)。
在$\triangle ABF$和$\triangle CDE$中:
$\begin{cases}AF = CE\\\angle AFB=\angle CED\\BF = DE\end{cases}$
根据$SAS$(两边及其夹角对应相等的两个三角形全等),可得$\triangle ABF\cong\triangle CDE$。
所以$AB = CD$,$\angle BAF=\angle DCE$,则$AB// CD$。
所以四边形$BEDF$是平行四边形(一组对边平行且相等的四边形是平行四边形)。
所以$DF = BE$且$DF// BE$。
综上,(1)得证$DE = BF$;(2)$DF = BE$且$DF// BE$。
查看更多完整答案,请扫码查看


