1. 阅读教科书第 43 页的内容后回答:观察例 1 的作图痕迹,并结合作法思考,为什么该作法是正确的?
(1) 由作法,你能得到哪些相等的线段?
(2) 要说明哪两个角相等?
(3) 要说明这两个角相等,需构造一对全等三角形,为此应添加怎样的辅助线?(请在下图中添加)
(4) 请你书写完整的证明过程。
- [img]
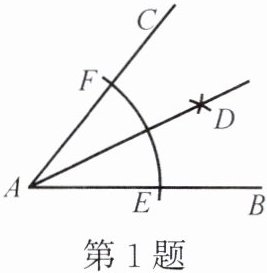
(1) 由作法,你能得到哪些相等的线段?
AF=AE(或FD=ED)
。(2) 要说明哪两个角相等?
∠CAD=∠BAD
。(3) 要说明这两个角相等,需构造一对全等三角形,为此应添加怎样的辅助线?(请在下图中添加)
DF,DE
(4) 请你书写完整的证明过程。
- [img]

提示:利用“SSS”证△ADF≌△ADE
答案:
(1)AF=AE(或FD=ED)(2)∠CAD=∠BAD(3)DF,DE(4)提示:利用“SSS”证△ADF≌△ADE
2. 阅读教科书第 44 页“做一做”及角平分线性质定理的内容后回答:
(1) 回顾关于点到直线的距离的定义。如图,点 P 到角两边的距离是指哪两条垂线段的长?
(2) 对照下图,请用几何语言写出角平分线性质定理:因为

(1) 回顾关于点到直线的距离的定义。如图,点 P 到角两边的距离是指哪两条垂线段的长?
PD,PE
。(2) 对照下图,请用几何语言写出角平分线性质定理:因为
∠PAC=∠PAD
,PE⊥AC
,PB⊥AB
,所以PE=PD
。
答案:
(1)PD,PE(2)∠PAC=∠PAD PE⊥AC PB⊥AB PE=PD
3. 阅读教科书第 44 页例 2 后回答:
(1) 例 2 为了证明 $ PA = PD $,不是直接证明这两条线段相等,而是分别证明它们与哪条线段相等?这种思考方法对你有怎样的启发?
(2) 教科书例 2 的解题思路是利用角平分线的性质证明 $ PA = PD $。延长 $ BP $,交 $ CD $ 于点 $ E $,你能否不用角平分线的性质,而用三角形全等的性质证明 $ PA = PD $? 请试一试。

(1) 例 2 为了证明 $ PA = PD $,不是直接证明这两条线段相等,而是分别证明它们与哪条线段相等?这种思考方法对你有怎样的启发?
(2) 教科书例 2 的解题思路是利用角平分线的性质证明 $ PA = PD $。延长 $ BP $,交 $ CD $ 于点 $ E $,你能否不用角平分线的性质,而用三角形全等的性质证明 $ PA = PD $? 请试一试。

答案:
(1)PE 两条线段相等有时不能直接证明,可以采用间接证明的方法;或是寻找(构造)与AP,DP相等的中间过渡的线段,或是构造分别以AP,DP为边的两个全等三角形
查看更多完整答案,请扫码查看


