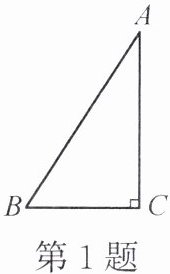
1. 在 $ Rt \triangle ABC $ 中,$ \angle C = 90^{\circ} $,至少用两种不同的方法作 $ \triangle A'B'C' $,使 $ \triangle A'B'C' \cong \triangle ABC $。

答案:
作图略,四种作法可以为 SSS,SAS,ASA,AAS
2. 有两条边和一个角对应相等的两个三角形全等吗?尝试用示意图说明。
答案:
不一定全等;如图,AB=AB,∠B=∠B,AD=AC,但△ABC 与△ABD 不全等
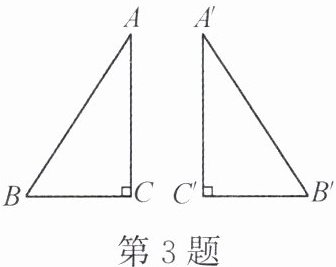
3. 阅读教科书中关于“$ HL $”的证明过程。教科书中的证明方法叫作“构造法”。对于这道题,你还有其他不同的证明思路吗?请写出来。
已知:
求证:
小贴士:(思路 1)先将 $ AB $ 与 $ A'B' $ 重合,再证明 $ Rt \triangle ABC \cong Rt \triangle A'B'C' $。(思路 2)利用勾股定理先证明 $ BC = B'C' $,再证明 $ Rt \triangle ABC \cong Rt \triangle A'B'C' $。

已知:
∠C=∠C'=90°,AB=A'B',AC=A'C'(或 BC=B'C')
。求证:
Rt△ABC≌Rt△A'B'C'
。小贴士:(思路 1)先将 $ AB $ 与 $ A'B' $ 重合,再证明 $ Rt \triangle ABC \cong Rt \triangle A'B'C' $。(思路 2)利用勾股定理先证明 $ BC = B'C' $,再证明 $ Rt \triangle ABC \cong Rt \triangle A'B'C' $。
证明略
答案:
已知:∠C=∠C'=90°,AB=A'B',AC=A'C'(或 BC=B'C') 求证:Rt△ABC≌Rt△A'B'C' 证明略
4. 如图,点 $ P $ 在 $ \angle BAC $ 的内部,$ PD \perp AB $ 于点 $ D $,$ PE \perp AC $ 于点 $ E $。

(1)若 $ AD = AE $,则 $ \triangle APD \cong \triangle APE $,理由是
(2)若 $ PD = 3 cm $,当 $ PE = $

(1)若 $ AD = AE $,则 $ \triangle APD \cong \triangle APE $,理由是
HL
。(2)若 $ PD = 3 cm $,当 $ PE = $
3
$ cm $ 时,$ AP $ 平分 $ \angle BAC $。
答案:
(1)HL (2)3
查看更多完整答案,请扫码查看


