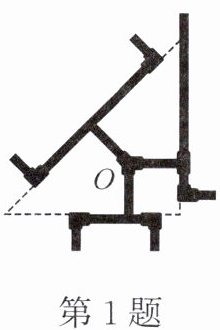
1. 如图所示是某油路管道的一部分,延伸外围的支路恰好构成一个直角三角形,两直角边长分别为 $ 6 m $ 和 $ 8 m $。按照输油中心 $ O $ 到三条支路的距离相等来连接管道,则 $ O $ 到三条支路的管道总长(计算时视管道为线,中心 $ O $ 为点)是
6
$ m $。
答案:
6
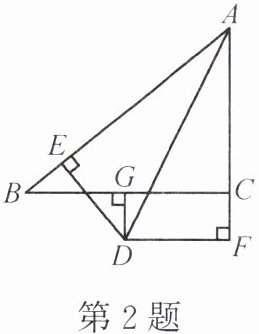
2. 如图,在 $ \triangle ABC $ 中,边 $ BC $ 的垂直平分线与 $ \angle BAC $ 的平分线交于点 $ D $,$ DE \perp AB $,$ DF \perp AC $,垂足分别为点 $ E $,$ F $。求证:$ BE = CF $。

答案:
提示:连结 BD,CD,证△BDE≌△CDF
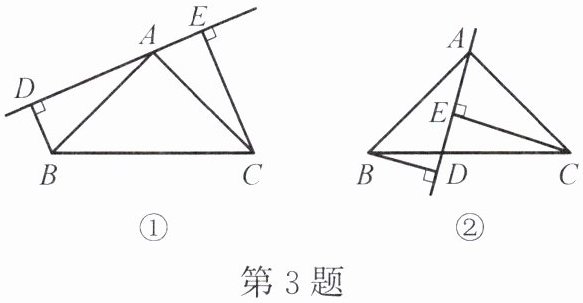
3. 如图,在 $ \triangle ABC $ 中,$ AB = AC $,$ DE $ 是过点 $ A $ 的直线,$ BD \perp DE $ 于点 $ D $,$ CE \perp DE $ 于点 $ E $。
(1)如图①,若 $ B $,$ C $ 在 $ DE $ 的同侧,且 $ AD = CE $。求证:$ AB \perp AC $。
(2)如图②,若 $ B $,$ C $ 在 $ DE $ 的两侧,且 $ AD = CE $,其他条件不变,则 $ AB $ 与 $ AC $ 仍垂直吗?若垂直,请给出证明;若不垂直,请说明理由。
(1)如图①,若 $ B $,$ C $ 在 $ DE $ 的同侧,且 $ AD = CE $。求证:$ AB \perp AC $。
(2)如图②,若 $ B $,$ C $ 在 $ DE $ 的两侧,且 $ AD = CE $,其他条件不变,则 $ AB $ 与 $ AC $ 仍垂直吗?若垂直,请给出证明;若不垂直,请说明理由。

答案:
(1)因为 BD⊥DE,CE⊥DE,所以∠ADB=∠AEC=90°。
因为 AB=AC,AD=CE,所以 Rt△ABD≌Rt△CAE。
所以∠DAB=∠ECA,∠DBA=∠EAC。
因为∠DAB+∠DBA=90°,∠EAC+∠ACE=90°,所以∠BAD+∠CAE=90°,∠BAC=180°-(∠BAD+∠CAE)=90°。所以 AB⊥AC
(2)AB⊥AC。理由:同
(1)可证得 Rt△ABD≌Rt△CAE。
所以∠DAB=∠ECA,∠DBA=∠EAC。因为∠CAE+∠ECA=90°,
所以∠CAE+∠BAD=90°,即∠BAC=90°。所以 AB⊥AC
因为 AB=AC,AD=CE,所以 Rt△ABD≌Rt△CAE。
所以∠DAB=∠ECA,∠DBA=∠EAC。
因为∠DAB+∠DBA=90°,∠EAC+∠ACE=90°,所以∠BAD+∠CAE=90°,∠BAC=180°-(∠BAD+∠CAE)=90°。所以 AB⊥AC
(2)AB⊥AC。理由:同
(1)可证得 Rt△ABD≌Rt△CAE。
所以∠DAB=∠ECA,∠DBA=∠EAC。因为∠CAE+∠ECA=90°,
所以∠CAE+∠BAD=90°,即∠BAC=90°。所以 AB⊥AC
查看更多完整答案,请扫码查看


