《2025年预学与导学八年级数学上册浙教版》

1. 若等腰三角形一条腰上的高线与另一条腰的夹角为 $ 30^{\circ} $,则它的顶角等于$60^{\circ}$或$120^{\circ}$。

答案： $60^{\circ}$或$120^{\circ}$

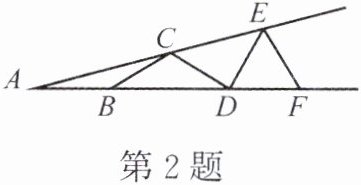
2. 如图,$ \angle A = 15^{\circ} $,$ AB = BC = CD = DE = EF $,则 $ \angle DEF $ 的度数为$60^{\circ}$。

答案： $60^{\circ}$

3. 如果等腰三角形的一个角的度数是另一个角的 $ 2 $ 倍少 $ 50^{\circ} $,那么它的顶角为$65^{\circ}$或$80^{\circ}$或$56^{\circ}$。

答案： $65^{\circ}$或$80^{\circ}$或$56^{\circ}$

4. 如图,在 $ \triangle ABC $ 中,$ AB = AC = 2 $,$ \angle B = 40^{\circ} $,点 $ D $ 在线段 $ BC $ 上运动(点 $ D $ 不与点 $ B $,$ C $ 重合),连结 $ AD $,作 $ \angle ADE = 40^{\circ} $,$ DE $ 交线段 $ AC $ 于点 $ E $。

(1) 当 $ \angle BDA = 115^{\circ} $ 时,$ \angle BAD = $$25^{\circ}$,$ \angle DEC = $$115^{\circ}$。
(2) 当 $ DC $ 等于多少时,$ \triangle ABD $ 与 $ \triangle DCE $ 全等？请说明理由。
（2）$DC=2$,理由略
(3) 在点 $ D $ 的运动过程中,$ \triangle ADE $的形状可以是等腰三角形吗？若可以,请直接写出 $ \angle BDA $ 的度数；若不可以,请说明理由。
（3）可以,$\angle BDA=80^{\circ}$或$110^{\circ}$

答案： （1）$25^{\circ}$ $115^{\circ}$ （2）$DC=2$,理由略 （3）可以,$\angle BDA=80^{\circ}$或$110^{\circ}$

5. 如图,在 $ \triangle ABC $ 中,$ AD $ 平分 $ \angle BAC $,$ AB + BD = AC $,猜想 $ \angle ABC $ 和 $ \angle C $的关系,并说明理由。

小贴士：线段和、差的问题通常可通过在长边上截取线段和在短边上补长线段的方法构造全等三角形来解决,这种方法称为截长补短法。

答案： $\angle ABC=2\angle C$。提示:在$AC$上截取$AE=AB$,连结$DE$