《2025年预学与导学八年级数学上册浙教版》

7. 在平面直角坐标系中,已知点$P$在第四象限,且到$x$轴的距离为13,到$y$轴的距离为12,则点$P$的坐标为(12,-13)。

答案： (12,-13)

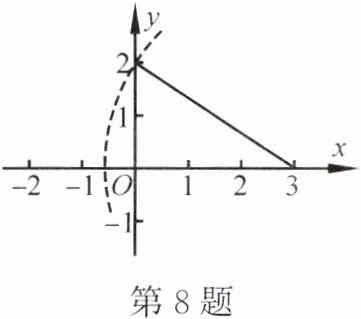
8. 如图,以点$(3,0)为圆心的圆弧与y轴交于点(0,2)$,与$x轴交于点P$,则点$P$的坐标为$(3-\sqrt{13},0)$。

答案： $(3-\sqrt{13},0)$

9. 在直角坐标系中,点$P(2-m,3m-1)关于x轴的对称点为M$,点$M关于y轴的对称点为Q$。若点$Q$在第三象限,则$m$的取值范围是$\frac{1}{3}＜m＜2$。

答案： $\frac{1}{3}＜m＜2$

10. 如图,将一块含有$45^{\circ}$角的三角尺放在平面直角坐标系中,使其顶点$C$,$B分别在x$轴、$y$轴上,如果点$A的坐标为(-3,1)$,那么点$B$的坐标为(0,2)。

答案： (0,2)

11. 定义：如图①,将射线$OX按逆时针方向旋转\beta$度,得到射线$OY$,如果$P为射线OY$上的一点,且$OP = a$,那么称$(a,\beta)为点P$的极坐标。

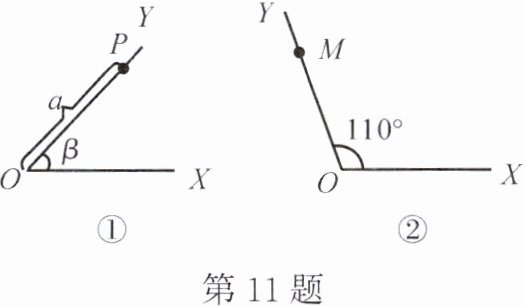
(1) 如图②,已知$OM = 8$,$\angle XOM = 110^{\circ}$,则点$M$的极坐标为(8,110)。
(2) 若点$H的极坐标为(2,1234)$,则点$H相对于点O$的位置可描述为H在O的北偏西$64^{\circ}$方向,距离O2处。

答案：
(1)(8,110)
(2)H在O的北偏西$64^{\circ}$方向,距离O2处

12. 在平面直角坐标系中,已知$O(0,0)$,$B(4,0)$,$C(-2,2\sqrt{3})$。
(1) $S_{\triangle BOC}$的面积为$4\sqrt{3}$。
(2) 点$B相对于点C$的位置可描述为B在C的南偏东$75^{\circ}$方向,距离C$\sqrt{48}$(即$4\sqrt{3}$)处。

答案：
(1)$4\sqrt{3}$
(2)B在C的南偏东$75^{\circ}$方向,距离C$\sqrt{48}$(即$4\sqrt{3}$)处

13. 如图,在平面直角坐标系中,已知$A(0,1)$,$B(2,0)$,$C(4,3)$。
(1) 在平面直角坐标系中,画出$\triangle ABC$。
(2) 在平面直角坐标系中,画出$\triangle ABC关于x轴对称的\triangle A_1BC_1$。
(3) 在平面直角坐标系中,画出$\triangle ABC$先向上平移2个单位长度,再向左平移5个单位长度所得的$\triangle A_2B_2C_2$。

答案：
(1) 在平面直角坐标系中，点$A(0,1)$，$B(2,0)$，$C(4,3)$，连接$A$，$B$，$C$三点，得到$\triangle ABC$。
(2) 点$A(0,1)$关于$x$轴对称的点$A_1(0,-1)$；
点$B(2,0)$关于$x$轴对称的点$B_1(2,0)$（因为$B$在$x$轴上，对称点与原点重合，仍为$B$，此处题目要求为$\triangle A_1BC_1$，所以$B$点不变）；
点$C(4,3)$关于$x$轴对称的点$C_1(4,-3)$；
连接$A_1$，$B$，$C_1$三点，得到$\triangle A_1BC_1$。
(3) 点$A(0,1)$先向上平移2个单位长度，再向左平移5个单位长度得到$A_2(-5,3)$；
点$B(2,0)$先向上平移2个单位长度，再向左平移5个单位长度得到$B_2(-3,2)$；
点$C(4,3)$先向上平移2个单位长度，再向左平移5个单位长度得到$C_2(-1,5)$；
连接$A_2$，$B_2$，$C_2$三点，得到$\triangle A_2B_2C_2$。