1. 在△ABC 中,AB= AC,BD 是边 AC 上的中线,BD 把△ABC 的周长分为 36 和 48 两部分,则 BC=
36 或 20
。
答案:
36 或 20
2. 已知△ABC 的面积为 S。
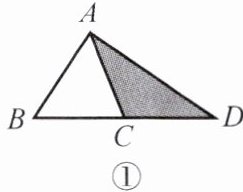
(1) 如图①,延长△ABC 的边 BC 到点 D,使 CD= BC,连结 DA。若△ACD 的面积为$ S_1,$则$ S_1= $
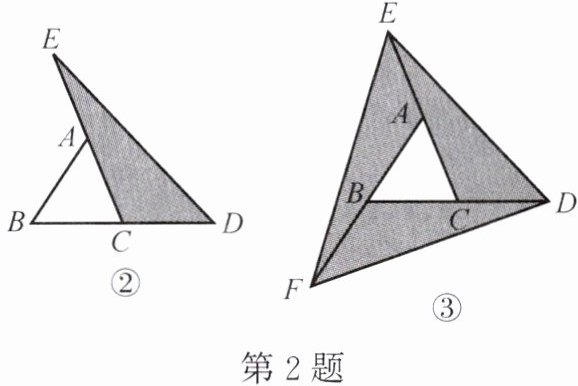
(2) 如图②,延长△ABC 的边 BC 到点 D,延长边 CA 到点 E,使 CD= BC,AE= CA,连结 DE。求△DEC 的面积$ S_2($用含 S 的代数式表示),并写出理由。
(3) 在图②的基础上延长 AB 到点 F,使 BF= AB,连结 FD,FE,得到△DEF,如图③。如果阴影部分的面积为$ S_3,$那么$ S_3= $
(1) 如图①,延长△ABC 的边 BC 到点 D,使 CD= BC,连结 DA。若△ACD 的面积为$ S_1,$则$ S_1= $
S
。(用含 S 的代数式表示)

(2) 如图②,延长△ABC 的边 BC 到点 D,延长边 CA 到点 E,使 CD= BC,AE= CA,连结 DE。求△DEC 的面积$ S_2($用含 S 的代数式表示),并写出理由。
2S,理由略
(3) 在图②的基础上延长 AB 到点 F,使 BF= AB,连结 FD,FE,得到△DEF,如图③。如果阴影部分的面积为$ S_3,$那么$ S_3= $
6S
。(用含 S 的代数式表示)
答案:
(1) S
(2) 2S,理由略
(3) 6S
(1) S
(2) 2S,理由略
(3) 6S
3. 在△ABC 中,∠A= 50°。
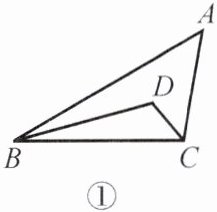
(1) 如图①,BD,CD 是△ABC 两个内角的平分线,两者相交于点 D,则∠BDC=
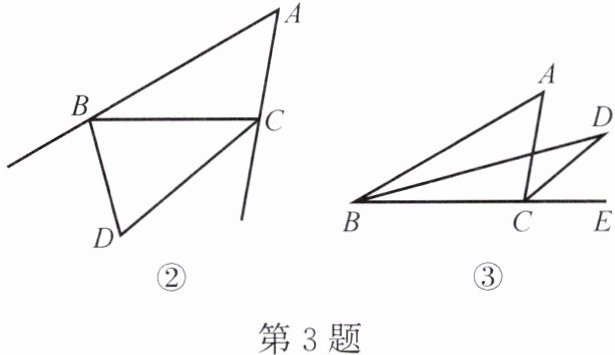
(2) 如图②,BD,CD 是△ABC 两个外角的平分线,两者相交于点 D,求∠BDC 的度数。
(3) 如图③,BD,CD 分别是△ABC 一个内角和一个外角的平分线,两者相交于点 D,求∠BDC 的度数。
(2) 65°
(3) 25°
(1) 如图①,BD,CD 是△ABC 两个内角的平分线,两者相交于点 D,则∠BDC=
115°
。
(2) 如图②,BD,CD 是△ABC 两个外角的平分线,两者相交于点 D,求∠BDC 的度数。
(3) 如图③,BD,CD 分别是△ABC 一个内角和一个外角的平分线,两者相交于点 D,求∠BDC 的度数。

(2) 65°
(3) 25°
答案:
(1) $115^{\circ}$
(2) $65^{\circ}$
(3) $25^{\circ}$
(1) $115^{\circ}$
(2) $65^{\circ}$
(3) $25^{\circ}$
查看更多完整答案,请扫码查看


