8. 求证:如果三角形的一个外角平分线平行于三角形的一边,那么这个三角形是等腰三角形。(请画出图形,写出已知、求证、证明过程)
答案:
如图,已知∠DAC是△ABC的外角,AE平分∠DAC,AE//BC。求证:△ABC为等腰三角形。证明提示:证∠B=∠C即可
1. 在 $ \triangle ABC $ 中,$ \angle A $ 的相邻外角是 $ 110° $,若 $ \triangle ABC $ 是等腰三角形,则 $ \angle B $ 的度数为
70°或40°或55°
。
答案:
70°或40°或55°
2. 如图,在等边三角形 $ ABC $ 中,点 $ D $,$ E $ 分别在边 $ AB $,$ BC $ 上,把 $ \triangle BDE $ 沿直线 $ DE $ 翻折,使点 $ B $ 落在点 $ B' $ 处,$ DB' $,$ EB' $ 分别交边 $ AC $ 于点 $ F $,$ G $。若 $ \angle ADF = 80° $,则 $ \angle EGC = $
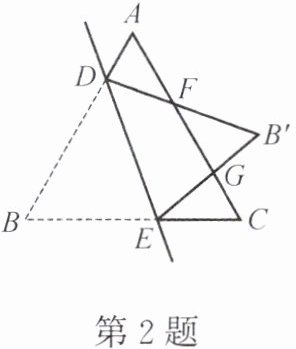
80°
。
答案:
80°
3. 如图,在 $ \triangle ABC $ 中,$ BF $,$ CF $ 都是角平分线,过点 $ F $ 作 $ DE // BC $,交 $ AB $ 于点 $ D $,交 $ AC $ 于点 $ E $。给出下列结论:①$ \triangle BDF $,$ \triangle BCF $,$ \triangle CEF $ 都是等腰三角形;②$ \triangle ADE $ 的周长等于 $ AB + AC $;③$ 2\angle BFC - \angle A = 180° $。其中正确的结论是
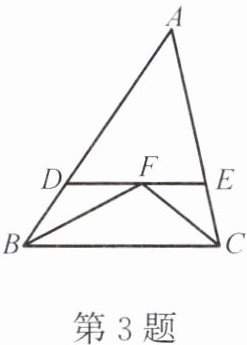
②③
。(填序号)
答案:
②③
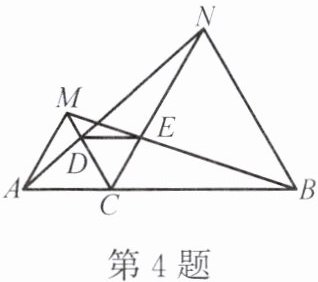
4. 如图,$ C $ 为线段 $ AB $ 上的一点,$ \triangle ACM $,$ \triangle CBN $ 都是等边三角形,连结 $ AN $ 和 $ BM $,分别交 $ MC $,$ NC $ 于点 $ D $,$ E $,连结 $ DE $。求证:
(1)$ AN = MB $。
(2)$ \triangle CDE $ 是等边三角形。
(1)$ AN = MB $。
(2)$ \triangle CDE $ 是等边三角形。

答案:
提示:
(1)证△ACN≌△MCB
(2)证△ACD≌△MCE,得CD=CE,再证△CDE为等边三角形
(1)证△ACN≌△MCB
(2)证△ACD≌△MCE,得CD=CE,再证△CDE为等边三角形
查看更多完整答案,请扫码查看


