1. 直角三角形的两个锐角满足怎样的关系?请证明。


答案:
两个锐角互余 提示:利用三角形的内角和定理证明
2. 阅读教科书中的本节内容后回答:
(1) 教科书本节内容中有一个直角三角形的重要性质:在直角三角形中,斜边上的中线等于斜边的一半。下面给出了一种证明方法,请把它补充完整。
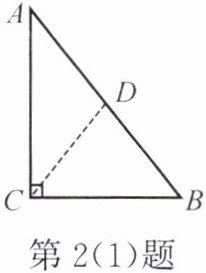
如图,在 $ Rt \triangle ABC $ 中, $ \angle ACB = 90^{\circ} $,求证:斜边上的中线等于斜边的一半。
证明:在斜边 $ AB $ 上取点 $ D $,连结 $ CD $,使得 $ \angle DCB = \angle B $。
所以 $ DC = $
因为 $ \angle ACB = 90^{\circ} $,
所以 $ \angle DCB + $
$ \angle A + $
所以
所以 $ DC = $
所以 $ DA = DC = DB $。
所以 $ DC = \frac{1}{2}AB $。
(2) 除了教科书中直角三角形的性质定理外,直角三角形还有一个重要的性质:在直角三角形中,如果有一个锐角等于 $ 30^{\circ} $,那么 $ 30^{\circ} $ 角所对的直角边等于斜边的一半。请仿照教科书中例 1 的证明方法证明该性质。
(1) 教科书本节内容中有一个直角三角形的重要性质:在直角三角形中,斜边上的中线等于斜边的一半。下面给出了一种证明方法,请把它补充完整。
如图,在 $ Rt \triangle ABC $ 中, $ \angle ACB = 90^{\circ} $,求证:斜边上的中线等于斜边的一半。
证明:在斜边 $ AB $ 上取点 $ D $,连结 $ CD $,使得 $ \angle DCB = \angle B $。
所以 $ DC = $
DB
。因为 $ \angle ACB = 90^{\circ} $,
所以 $ \angle DCB + $
∠DCA
$ = 90^{\circ} $,$ \angle A + $
∠DCB
$ = 90^{\circ} $。所以
∠DCA
$ = \angle A $。所以 $ DC = $
DA
。所以 $ DA = DC = DB $。
所以 $ DC = \frac{1}{2}AB $。

(2) 除了教科书中直角三角形的性质定理外,直角三角形还有一个重要的性质:在直角三角形中,如果有一个锐角等于 $ 30^{\circ} $,那么 $ 30^{\circ} $ 角所对的直角边等于斜边的一半。请仿照教科书中例 1 的证明方法证明该性质。
(2)略
答案:
(1) DB ∠DCA ∠DCB ∠DCA DA
(2)略
(1) DB ∠DCA ∠DCB ∠DCA DA
(2)略
3. 阅读教科书的本节内容后回答:
(1) 在 $ \triangle ABC $ 中,已知 $ \angle C = 90^{\circ} $, $ \angle A : \angle B = 2 : 3 $,则 $ \angle A = $
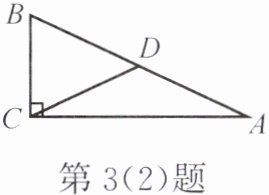
(2) 如图,在 $ Rt \triangle ABC $ 中, $ \angle ACB = 90^{\circ} $, $ AB = 10 $, $ D $ 是斜边的中点,连结 $ CD $。若 $ \angle ACD = 25^{\circ} $,则 $ CD = $
(1) 在 $ \triangle ABC $ 中,已知 $ \angle C = 90^{\circ} $, $ \angle A : \angle B = 2 : 3 $,则 $ \angle A = $
36°
, $ \angle B = $54°
。(2) 如图,在 $ Rt \triangle ABC $ 中, $ \angle ACB = 90^{\circ} $, $ AB = 10 $, $ D $ 是斜边的中点,连结 $ CD $。若 $ \angle ACD = 25^{\circ} $,则 $ CD = $
5
, $ \angle B = $65°
。
答案:
(1)36° 54°
(2)5 65°
(1)36° 54°
(2)5 65°
查看更多完整答案,请扫码查看


