1. 满足不等式$-\pi \leq x < \sqrt{2}的x$的整数值有
-3,-2,-1,0,1
。
答案:
-3,-2,-1,0,1
2. 如图,若数轴上的两点$A$,$B表示的数分别为a$,$b$,则下列结论正确的是(

A.$a - b > 0$
B.$\frac{1}{2}b - a > 0$
C.$2a + b > 0$
D.$a + b > 0$
小贴士:有困难的同学可以尝试用特殊值法来判断。
B
)。
A.$a - b > 0$
B.$\frac{1}{2}b - a > 0$
C.$2a + b > 0$
D.$a + b > 0$
小贴士:有困难的同学可以尝试用特殊值法来判断。
答案:
B
3. 目前常用的一种评定肥胖程度的方法为测试人的体重指数($BMI$),$BMI= \frac{体重(kg)}{身高^{2}(m^{2})}$。一般而言,当一个人的体重指数为$18 \sim 24$(包括$18和24$)时,这个人的体重正常。设某人的$BMI为x$。
(1)用不等式表示$BMI$的正常指数范围,并把它表示在数轴上。
(2)下列值为$4个人的BMI$,他们的体重正常吗?用不等式和数轴说明理由。
①$x_{1} = 16$,②$x_{2} = 17.5$,③$x_{3} = 22$,④$x_{4} = 28$。
(1)用不等式表示$BMI$的正常指数范围,并把它表示在数轴上。
(2)下列值为$4个人的BMI$,他们的体重正常吗?用不等式和数轴说明理由。
①$x_{1} = 16$,②$x_{2} = 17.5$,③$x_{3} = 22$,④$x_{4} = 28$。
答案:
(1)18≤x≤24,数轴略 (2)①②④不正常,③正常,数轴略
4. 阅读下列材料,回答问题:
从图①所示的数轴上看:大于$-3而小于3的数的绝对值小于3$,即$\vert x\vert < 3$。
从图②所示的数轴上看:小于$-3或大于3的数的绝对值大于3$,即$\vert x\vert > 3$。
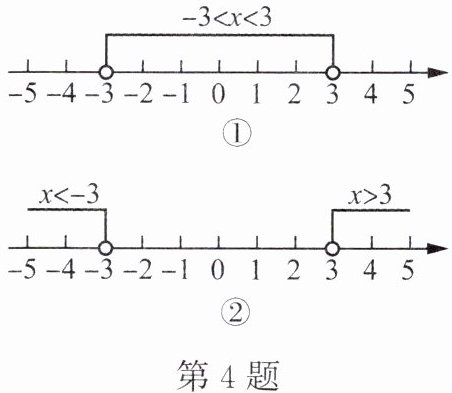
(1)满足不等式$\vert x\vert < a(a > 0)的x$的取值范围是
(2)利用数轴写出满足不等式$\vert x - 5\vert < 3的x$的取值范围。
从图①所示的数轴上看:大于$-3而小于3的数的绝对值小于3$,即$\vert x\vert < 3$。
从图②所示的数轴上看:小于$-3或大于3的数的绝对值大于3$,即$\vert x\vert > 3$。

(1)满足不等式$\vert x\vert < a(a > 0)的x$的取值范围是
-a<x<a
,满足不等式$\vert x\vert > a(a > 0)的x$的取值范围是x>a或x<-a
。(2)利用数轴写出满足不等式$\vert x - 5\vert < 3的x$的取值范围。
2<x<8,图略
答案:
(1)-a<x<a x>a或x<-a (2)2<x<8,图略
查看更多完整答案,请扫码查看


