1. 如图,在 $ Rt \triangle ABC $ 中, $ CD $ 是斜边 $ AB $ 上的中线,则图中与 $ CD $ 一定相等的线段有(
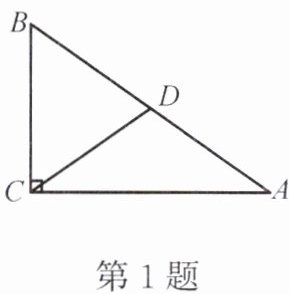
A.$ AD $ 与 $ BD $
B.$ BD $ 与 $ BC $
C.$ AD $ 与 $ BC $
D.$ AD $, $ BD $ 与 $ BC $
A
)。
A.$ AD $ 与 $ BD $
B.$ BD $ 与 $ BC $
C.$ AD $ 与 $ BC $
D.$ AD $, $ BD $ 与 $ BC $
答案:
A
2. 如图,已知 $ \triangle ABC $ 为直角三角形, $ \angle C = 90^{\circ} $,若沿图中虚线剪去 $ \angle C $,则 $ \angle 1 + \angle 2 $等于

270
度。
答案:
270
3. 如图,每个小正方形的边长为 1,点 $ A $, $ B $, $ C $ 是小正方形的顶点,则 $ \angle ABC = $
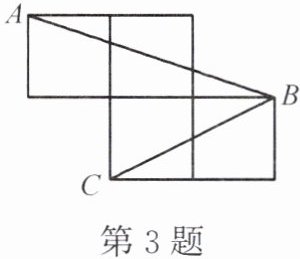
45
度。
答案:
45
4. 如图,已知 $ \angle ACB = 90^{\circ} $, $ CD \perp AB $,垂足为点 $ D $。给出下列结论:①图中有 3 个直角三角形,② $ \angle 1 = \angle 2 $,③ $ \angle 1 $ 和 $ \angle B $ 都是 $ \angle A $ 的余角,④ $ \angle 2 = \angle A $。其中正确的结论有

①③④
。(填序号)
答案:
①③④
5. 已知直角三角形斜边上的高线与中线长分别为 $ 4 cm $, $ 5 cm $,则此直角三角形的面积是
20 cm²
。
答案:
20 cm²
6. 如图,在 $ Rt \triangle ABC $ 中, $ \angle C = 90^{\circ} $, $ AB $ 的垂直平分线交 $ AC $ 于点 $ D $,交 $ AB $ 于点 $ E $, $ BD $ 平分 $ \angle ABC $。求 $ \angle A $, $ \angle ABC $ 的度数。


答案:
∠A=30°,∠ABC=60°
7. 如图所示是由一副三角尺拼成的四边形 $ ABCD $, $ E $ 为 $ BD $ 的中点。试判断 $ AE $ 与 $ CE $ 的大小关系,并说明理由。


答案:
提示:在Rt△ABE中,AE>BE;在Rt△BCE中,CE=BE,故AE>CE
查看更多完整答案,请扫码查看


