1. 下列命题的条件和结论分别是什么?判断这些命题是否正确。
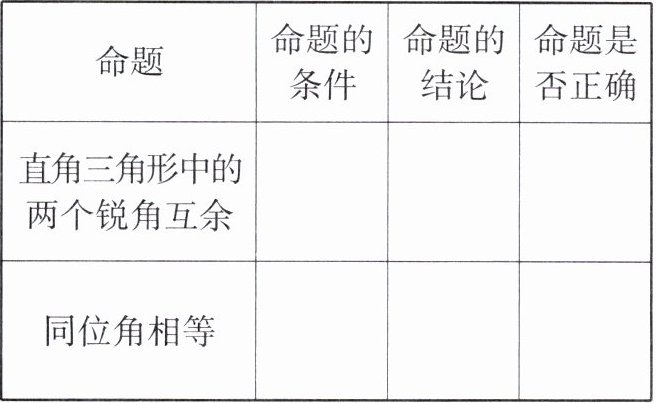

两个角是直角三角形的两个锐角,这两个角互余,正确;两个角是同位角,这两个角相等,不正确。
答案:
两个角是直角三角形的两个锐角,这两个角互余,正确;两个角是同位角,这两个角相等,不正确。
2. 阅读教科书中的本节内容后回答:
(1)命题的反例的作用:反例可以说明一个命题为
(2)当两个角的度数分别为
(3)“对顶角相等”是
(4)命题的反例是具备命题的条件,但不具备命题结论的实例。因此,举反例需要遵循一定的格式。请参照例2的(2)和(3)的解答过程,说明命题“若$a + b = c$,则$c > a$,$c > b$”是假命题。
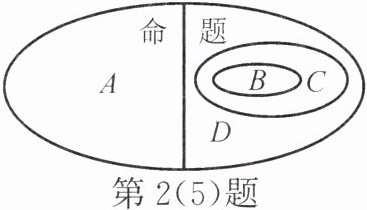
(5)思考真命题、基本事实、定理三者之间的区别与联系。真命题、假命题、基本事实、定理之间的关系如图所示,则$A$表示
(1)命题的反例的作用:反例可以说明一个命题为
假命题
。(2)当两个角的度数分别为
90°
、90°
时,可以作为反例来说明命题“如果两个角互补,那么这两个角一个是锐角,另一个是钝角”为假命题。(3)“对顶角相等”是
定理
。(填“定义”“基本事实”或“定理”)(4)命题的反例是具备命题的条件,但不具备命题结论的实例。因此,举反例需要遵循一定的格式。请参照例2的(2)和(3)的解答过程,说明命题“若$a + b = c$,则$c > a$,$c > b$”是假命题。
例如,取a = -1,b = -2,则c = (-1) + (-2) = -3 < -2 < -1,即c < a,c < b
(5)思考真命题、基本事实、定理三者之间的区别与联系。真命题、假命题、基本事实、定理之间的关系如图所示,则$A$表示
假命题
,$B$表示基本事实
,$C$表示定理
,$D$表示真命题
。
答案:
(1)假命题
(2)90° 90°
(3)定理
(4)例如,取a = -1,b = -2,则c = (-1) + (-2) = -3 < -2 < -1,即c < a,c < b
(5)假命题,基本事实,定理,真命题
(1)假命题
(2)90° 90°
(3)定理
(4)例如,取a = -1,b = -2,则c = (-1) + (-2) = -3 < -2 < -1,即c < a,c < b
(5)假命题,基本事实,定理,真命题
1. 下列命题中,为真命题的是(
A.锐角大于它的余角
B.锐角大于它的补角
C.钝角大于它的补角
D.锐角与钝角之和等于平角
C
)。A.锐角大于它的余角
B.锐角大于它的补角
C.钝角大于它的补角
D.锐角与钝角之和等于平角
答案:
C
2. 下列说法中,正确的是(
A.命题一定是正确的
B.不正确的判断不是命题
C.真命题都是基本事实
D.定理都是真命题
D
)。A.命题一定是正确的
B.不正确的判断不是命题
C.真命题都是基本事实
D.定理都是真命题
答案:
D
3. 甲、乙两人讨论“对顶角不相等”是不是命题。甲认为:这不是命题,因为这句话是错误的。乙认为:这是命题,因为它作出了判断,只不过这一判断是错误的,所以它是假命题。这两人的看法中,你认为(
A.甲正确
B.乙正确
C.甲、乙都正确
D.甲、乙都不正确
B
)。A.甲正确
B.乙正确
C.甲、乙都正确
D.甲、乙都不正确
答案:
B
查看更多完整答案,请扫码查看


