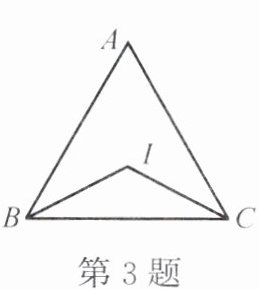
3. 如图,等边三角形 $ ABC $ 的两条角平分线相交于点 $ I $,则 $ \angle BIC = $
120
度。
答案:
120
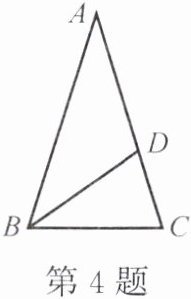
4. 如图,在 $ \triangle ABC $ 中,$ AB = AC $,$ BD $ 是 $ \angle ABC $ 的平分线。如果 $ \angle A = 40^{\circ} $,那么 $ \angle BDA = $
$105^{\circ}$
。
答案:
$105^{\circ}$
5. 若等腰三角形的一个内角为 $ 50^{\circ} $,则这个等腰三角形的底角为
$50^{\circ}$或$65^{\circ}$
。
答案:
$50^{\circ}$或$65^{\circ}$
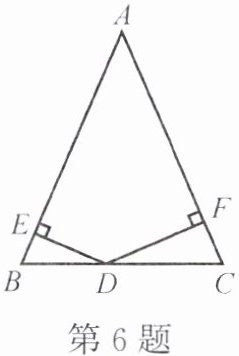
6. 如图,在 $ \triangle ABC $ 中,$ AB = AC $,$ D $ 是边 $ BC $ 上的一点,$ DE \perp AB $,$ DF \perp AC $,垂足分别为点 $ E $,$ F $,可以添加一个条件:
$BD=CD$或$BE=CF$
,使 $ DE = DF $。
答案:
$BD=CD$或$BE=CF$
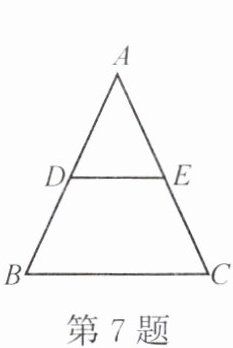
7. 如图,在 $ \triangle ABC $ 中,$ AB = AC $,$ D $,$ E $ 分别是边 $ AB $,$ AC $ 上的点,且 $ AD = AE $。求证:$ DE // BC $。

答案:
提示:证$\angle ADE=\angle B$
8. 如图,$ \triangle ABC $ 和 $ \triangle EBD $ 均为等边三角形,点 $ D $ 在边 $ BC $ 上。求证:$ AD = CE $。
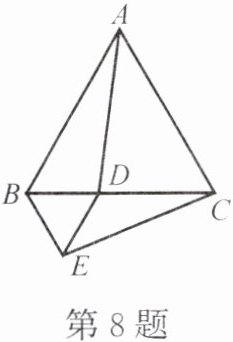

答案:
提示:证$\triangle ABD\cong\triangle CBE$
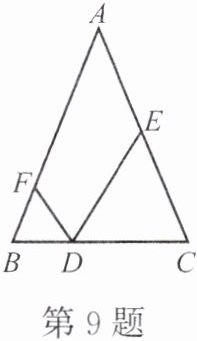
9. 如图,已知 $ \triangle ABC $ 为等腰三角形,$ AB = AC $,点 $ D $,$ E $,$ F $ 分别在 $ BC $,$ AC $,$ AB $ 上,且 $ CE = CD $,$ BD = BF $。
(1) 若 $ \angle A = 40^{\circ} $,求 $ \angle EDF $ 的度数。
(2) 试探究 $ \angle A $ 与 $ \angle EDF $ 之间的数量关系。
(1) 若 $ \angle A = 40^{\circ} $,求 $ \angle EDF $ 的度数。
(2) 试探究 $ \angle A $ 与 $ \angle EDF $ 之间的数量关系。

答案:
(1)$70^{\circ}$ (2)$\angle A+2\angle EDF=180^{\circ}$
查看更多完整答案,请扫码查看


