1. 等腰三角形的对称轴是
操作:把等腰三角形按如图所示的方式对折后再复原。

结论:
(1) $ \triangle ABD $ 与 $ \triangle ACD $
(2) $ \angle ABC $ 与 $ \angle ACB $
顶角的平分线(底边上的中线或高)所在的直线
。操作:把等腰三角形按如图所示的方式对折后再复原。

结论:
(1) $ \triangle ABD $ 与 $ \triangle ACD $
全等
,理由:全等的定义
。(2) $ \angle ABC $ 与 $ \angle ACB $
相等
,理由:重合或全等三角形对应角相等
。
答案:
顶角的平分线(底边上的中线或高)所在的直线 (1)全等 全等的定义 (2)相等 重合或全等三角形对应角相等
2. 阅读教科书中的本节内容后回答:
(1) 在 $ \triangle ABC $ 中,$ AB = AC $,已知 $ \angle A $的度数,求 $ \angle ABC $ 的度数,有公式:$ \angle ABC = $
(2) 若等腰三角形的一个顶角为 $ 70^{\circ} $,则底角为
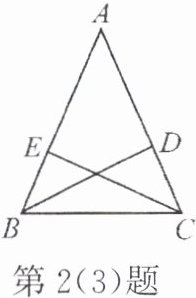
(3) 对于教科书中的例 2,你还有其他证明方法吗?若有,请写出证明过程。
(1) 在 $ \triangle ABC $ 中,$ AB = AC $,已知 $ \angle A $的度数,求 $ \angle ABC $ 的度数,有公式:$ \angle ABC = $
$\frac{180^{\circ}-\angle A}{2}$
;同理,已知 $ \angle ABC $ 的度数,求 $ \angle A $的度数,有公式:$ \angle A = $$180^{\circ}-2\angle ABC$
。(2) 若等腰三角形的一个顶角为 $ 70^{\circ} $,则底角为
55
度;若等腰三角形的一个底角为 $ 70^{\circ} $,则顶角为40
度。(3) 对于教科书中的例 2,你还有其他证明方法吗?若有,请写出证明过程。

证明$\triangle ABD\cong\triangle ACE$
答案:
(1)$\frac{180^{\circ}-\angle A}{2}$ $180^{\circ}-2\angle ABC$ (2)55 40 (3)证明$\triangle ABD\cong\triangle ACE$
1. 如图,在等边三角形 $ ABC $ 中,$ CD \perp AB $ 于点 $ D $,则 $ \angle ACD = $

30
度。
答案:
30
2. 如图,$ \triangle ABC $ 是等边三角形,延长 $ BC $至点 $ D $,使 $ CD = AC $,连结 $ AD $,则 $ \angle BAD = $
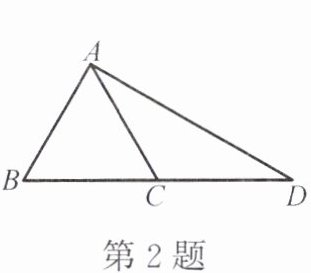
90
度。
答案:
90
查看更多完整答案,请扫码查看


