《2025年预学与导学八年级数学上册浙教版》

4. 下列不能作为反例来说明命题“若$a ＜ b$,则$\frac{1}{a} ＜ \frac{1}{b}$”为假命题的是(A)。
A.$a = 2$,$b = 3$
B.$a = -2$,$b = -1$
C.$a = -3$,$b = 2$
D.$a = -3$,$b = -2$

答案： A

5. 给出下列命题：①两条直线相交,只有一个交点；②三角形的内角和为$180^{\circ}$；③任何数的零次幂都等于$1$；④两个无理数的乘积一定是无理数。其中真命题有①②。(填序号)

答案： ①②

6. 判断下列命题的真假,并说明理由。
(1)大于$90^{\circ}$的角是钝角。
(2)若$x^{2} = 1$,则$x = 1$。
(3)如果$ab ＞ 0$,那么$a ＞ 0$,$b ＞ 0$。
(4)在$\triangle ABC$中,若$\angle A + \angle B = 90^{\circ}$,则$\angle C = \angle A + \angle B$。

答案：
(1)假命题。如180° ＞ 90°，但180°角是平角，不是钝角。
(2)假命题。如(-1)² = 1，但-1 ≠ 1。
(3)假命题。取a = -1，b = -2，则(-1)×(-2) ＞ 0，但a ＜ 0，b ＜ 0。
(4)真命题。∠C = 90° = ∠A + ∠B。

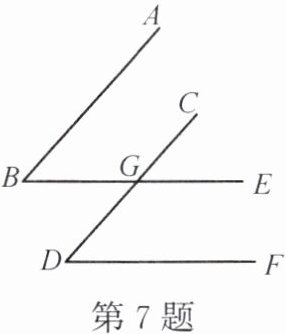
7. 如图,已知$\angle ABE的边BE与\angle CDF的边DC交于点G$,现有三个论断：①$AB // CD$,②$BE // DF$,③$\angle B = \angle D$。请你以其中两个论断作为条件,另外一个论断作为结论,写出所有的命题,然后判断这些命题是真命题还是假命题,并选择其中一个真命题加以论证。

答案： ①②→③真命题；①③→②真命题；②③→①真命题。证明略。