1. 如图,在△ABC中,AB= AC,BE= CE,则由“SSS”可以判定(
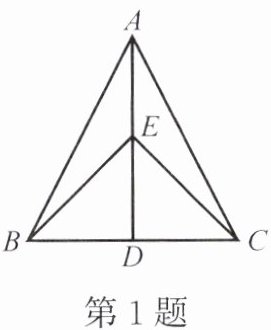
A.△ABD≌△ACD
B.△BDE≌△CDE
C.△ABE≌△DBE
D.△ABE≌△ACE
D
)。
A.△ABD≌△ACD
B.△BDE≌△CDE
C.△ABE≌△DBE
D.△ABE≌△ACE
答案:
D
2. 如图,已知AB= AD,BE= DE,BC= DC,则图中全等的三角形有(
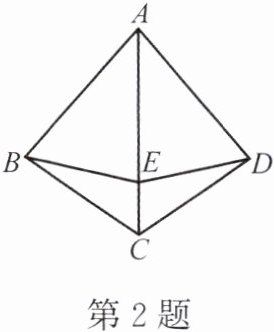
A.1对
B.2对
C.3对
D.4对
C
)。
A.1对
B.2对
C.3对
D.4对
答案:
C
3. 如图,王师傅用4根木条钉成一个四边形框架,要使这个框架不变形,他至少还要再钉木条(
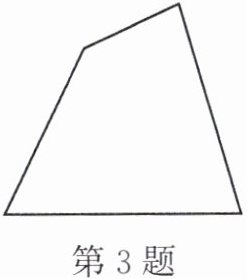
A.0根
B.1根
C.2根
D.3根
B
)。
A.0根
B.1根
C.2根
D.3根
答案:
B
4. 如图,AB= CD,BC= AD,则△ABC≌△
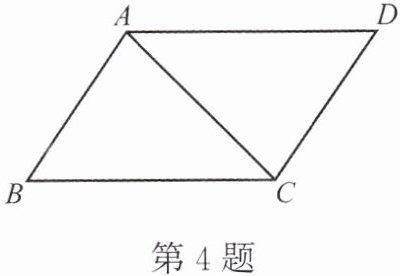
CDA
,理由是SSS
。
答案:
CDA SSS
5. 如图,点B,D,C,F在同一直线上,且BC= FD,AB= EF,AC= ED。求证:AC//DE。(填空)
证明:在△ABC和△EFD中,
因为AC=
所以
所以∠ACB=
所以
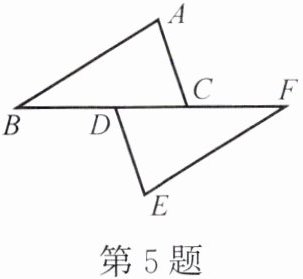
证明:在△ABC和△EFD中,
因为AC=
ED
,AB=EF,BC=FD
所以
△ABC
≌△EFD
(SSS
)。所以∠ACB=
∠EDF
(全等三角形的对应角相等
)。所以
AC
//DE(内错角相等,两直线平行
)。
答案:
ED BC △ABC △EFD SSS ∠EDF 全等三角形的对应角相等 AC 内错角相等,两直线平行
6. 如图,在四边形ABCD中,AB= CB,AD= CD,∠ABC= 110°,求∠ABD的度数。
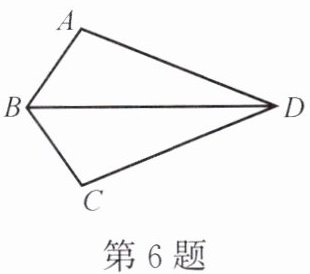

答案:
55°
7. (1) 用直尺和圆规作△ABC,使得AB= 4cm,AC= 2cm,BC= 3cm。
(2) 在第(1)题的边AB上取一点D(不与点A,B重合),用直尺和圆规过点D作DE//BC,交AC于点E。
(2) 在第(1)题的边AB上取一点D(不与点A,B重合),用直尺和圆规过点D作DE//BC,交AC于点E。
答案:
(1) ①作线段AB=4cm;②以A为圆心,2cm为半径画弧;③以B为圆心,3cm为半径画弧,两弧交于点C;④连接AC、BC,△ABC即为所求。
(2) ①在AB上取点D(不与A、B重合);②以B为圆心,任意长为半径画弧,交BA、BC于M、N;③以D为圆心,BM长为半径画弧,交DA于P;④以P为圆心,MN长为半径画弧,交前弧于Q;⑤过D、Q作射线DE交AC于E,DE//BC即为所求。
(1) ①作线段AB=4cm;②以A为圆心,2cm为半径画弧;③以B为圆心,3cm为半径画弧,两弧交于点C;④连接AC、BC,△ABC即为所求。
(2) ①在AB上取点D(不与A、B重合);②以B为圆心,任意长为半径画弧,交BA、BC于M、N;③以D为圆心,BM长为半径画弧,交DA于P;④以P为圆心,MN长为半径画弧,交前弧于Q;⑤过D、Q作射线DE交AC于E,DE//BC即为所求。
查看更多完整答案,请扫码查看


