1. 如图,已知∠B = ∠D = 90°,∠C = ∠E,AB = AD。给出下列结论:①BM = DN,②EM = CF,③∠BAM = ∠DAN,④△ACM ≌ △AEN。其中正确的结论是

①③④
。(填序号)
答案:
①③④
2. 如图,点E在△ABC的外部,点D在边BC上,DE交AC于点F。若∠1 = ∠2 = ∠3,AC = AE,求证:AB = AD。
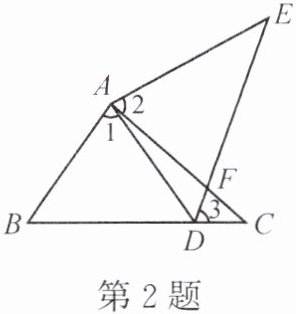

答案:
提示:证△ABC≌△ADE
3. 如图,CD ⊥ AB,BE ⊥ AC,垂足分别为点D,E,BE与CD相交于点O,且BE = CD。
(1) 求证:BD = CE。
(2) 连结AO,求证:AO平分∠BAC。

(1) 求证:BD = CE。
(2) 连结AO,求证:AO平分∠BAC。

答案:
1. (1)证明:
因为$CD\perp AB$,$BE\perp AC$,所以$\angle BDO=\angle CEO = 90^{\circ}$。
在$\triangle BDO$和$\triangle CEO$中,$\angle BOD=\angle COE$(对顶角相等),$\angle BDO=\angle CEO$,$BE = CD$。
根据$AAS$(两角及其中一角的对边对应相等的两个三角形全等),可得$\triangle BDO\cong\triangle CEO$。
由全等三角形的对应边相等,所以$BD = CE$。
2. (2)证明:
因为$\triangle BDO\cong\triangle CEO$,所以$OD = OE$。
又因为$OD\perp AB$,$OE\perp AC$。
根据角平分线的判定定理(到角两边距离相等的点在角的平分线上),所以$AO$平分$\angle BAC$。
综上,(1)$BD = CE$得证;(2)$AO$平分$\angle BAC$得证。
因为$CD\perp AB$,$BE\perp AC$,所以$\angle BDO=\angle CEO = 90^{\circ}$。
在$\triangle BDO$和$\triangle CEO$中,$\angle BOD=\angle COE$(对顶角相等),$\angle BDO=\angle CEO$,$BE = CD$。
根据$AAS$(两角及其中一角的对边对应相等的两个三角形全等),可得$\triangle BDO\cong\triangle CEO$。
由全等三角形的对应边相等,所以$BD = CE$。
2. (2)证明:
因为$\triangle BDO\cong\triangle CEO$,所以$OD = OE$。
又因为$OD\perp AB$,$OE\perp AC$。
根据角平分线的判定定理(到角两边距离相等的点在角的平分线上),所以$AO$平分$\angle BAC$。
综上,(1)$BD = CE$得证;(2)$AO$平分$\angle BAC$得证。
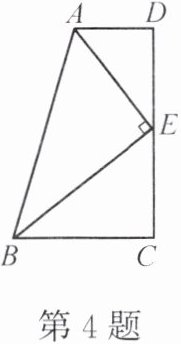
4. 如图,在四边形ABCD中,AD // BC,E为CD的中点,连结AE,BE,BE ⊥ AE。求证:AB = BC + AD。
小贴士:证明线段a + b = c的常用方法是“截长补短”。
小贴士:证明线段a + b = c的常用方法是“截长补短”。

答案:
延长AE,交BC延长线于点F,先证△ADE≌△FCE,得AE=FE,AD=FC,再证AB=BF
查看更多完整答案,请扫码查看


