1. 如图,已知 $ AB = AD $,添加下列条件后,仍无法判定 $ \triangle ABC \cong \triangle ADC $ 的是(
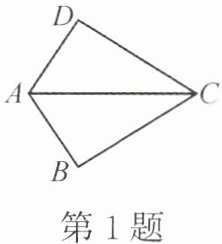
A.$ CB = CD $
B.$ \angle BAC = \angle DAC $
C.$ \angle BCA = \angle DCA $
D.$ \angle B = \angle D = 90^{\circ} $
C
)。
A.$ CB = CD $
B.$ \angle BAC = \angle DAC $
C.$ \angle BCA = \angle DCA $
D.$ \angle B = \angle D = 90^{\circ} $
答案:
C
2. 下列条件中,不能判定两个直角三角形全等的是(
A.一条直角边和一个锐角分别相等
B.两条直角边对应相等
C.斜边和一条直角边对应相等
D.两个锐角对应相等
D
)。A.一条直角边和一个锐角分别相等
B.两条直角边对应相等
C.斜边和一条直角边对应相等
D.两个锐角对应相等
答案:
D
3. 如图,已知在 $ \triangle ABC $ 中,$ \angle C = 90^{\circ} $,$ \angle ABC $ 的平分线 $ BD $ 交 $ AC $ 于点 $ D $。如果 $ BD = 10 cm $,$ BC = 8 cm $,那么点 $ D $ 到直线 $ AB $ 的距离是
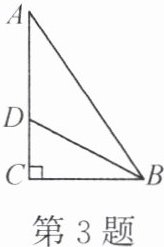
6
$ cm $。
答案:
6
4. 给出下列命题:①一个锐角和一条斜边分别相等的两个直角三角形全等,②一个锐角和一条边分别相等的两个直角三角形全等,③两边分别对应相等的两个直角三角形全等,④一条直角边和一条斜边分别对应相等的两个直角三角形全等。其中正确的命题有
①④
。(填序号)
答案:
①④
5. 如图,$ PA $,$ PC $ 分别是 $ \triangle ABC $ 的外角 $ \angle MAC $ 与 $ \angle NCA $ 的平分线,且交于点 $ P $,$ PD \perp BM $,垂足为点 $ D $,$ PF \perp BN $,垂足为点 $ F $。求证:$ BP $ 为 $ \angle MBN $ 的平分线。


答案:
提示:过点 P 作 AC 的垂线,利用角平分线的性质定理及逆定理得证
6. 如图,已知 $ AB = AC $,$ CD \perp AB $ 于点 $ D $,$ BE \perp AC $ 于点 $ E $,$ BE $ 与 $ CD $ 相交于点 $ O $。
(1)图中有几对全等的直角三角形?请你选择其中一对进行证明。
(2)连结 $ OA $,$ BC $,试判断直线 $ OA $ 与 $ BC $ 的位置关系,并说明理由。
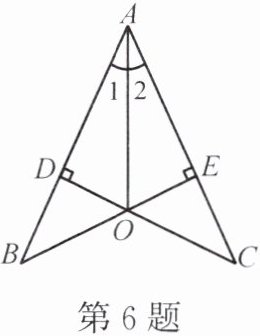
(1)图中有几对全等的直角三角形?请你选择其中一对进行证明。
(2)连结 $ OA $,$ BC $,试判断直线 $ OA $ 与 $ BC $ 的位置关系,并说明理由。

答案:
(1)△ABE≌△ACD,△ADO≌△AEO,△DOB≌△EOC,证明略
(2)AO 垂直 BC 且平分线段 BC。提示:连结 AO 并延长,交 BC 于点 F,证△DBO≌△ECO,得 BO=CO,由垂直平分线定理的逆定理证得结论
(2)AO 垂直 BC 且平分线段 BC。提示:连结 AO 并延长,交 BC 于点 F,证△DBO≌△ECO,得 BO=CO,由垂直平分线定理的逆定理证得结论
查看更多完整答案,请扫码查看


