1. 如图,在△ABC中,AB= AC,∠BAC= 60°,D是△ABC外一点,∠ACD= 30°,∠BAC的平分线AE交BD于点E,且AE= AD,BE= CD,则∠AED=

60°
,∠BAD= 90°
。
答案:
60° 90°
2. 如图,已知AB= AC,AD= AE,BD= CE,请找出图中的全等三角形,并证明其中的一对三角形全等。


答案:
△ABD≌△ACE,△ABE≌△ACD,证明略
3. 为了参加学校举行的风筝设计比赛,小慧用四根竹棒扎成如图所示的风筝框架,已知AB= DC,AC= DB。小慧制作的风筝两个“脚”大小相等(即∠B= ∠C)吗?试说明理由。
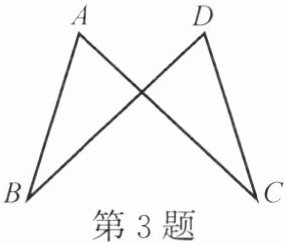

答案:
相等,提示:连结AD,证△ABD≌△DCA
4. 如图,已知△ABE≌△ACD,点D,E分别在AB,AC上。
(1) 求证:∠1= ∠2。
(2) 连结BC,求证:BC//DE。
小贴士:利用三角形全等的性质可以证明线段相等或者角相等。图中∠1与∠2分别位于哪两个三角形中?试判断这两个三角形是否全等。
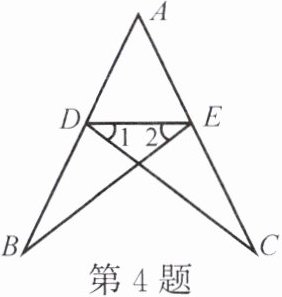
(1) 求证:∠1= ∠2。
(2) 连结BC,求证:BC//DE。
小贴士:利用三角形全等的性质可以证明线段相等或者角相等。图中∠1与∠2分别位于哪两个三角形中?试判断这两个三角形是否全等。

答案:
1. (1)证明$\angle1 = \angle2$:
因为$\triangle ABE\cong\triangle ACD$,根据全等三角形的性质,全等三角形的对应边相等,对应角相等,所以$AB = AC$,$AD = AE$,$\angle B=\angle C$。
又因为$AB = AC$,$AD = AE$,所以$AB - AD=AC - AE$,即$BD = CE$。
在$\triangle BDE$和$\triangle CED$中:
$\left\{\begin{array}{l}BD = CE\\\angle B=\angle C\\BE = CD\end{array}\right.$(由$\triangle ABE\cong\triangle ACD$得$BE = CD$)。
根据$SAS$(边角边)判定定理,$\triangle BDE\cong\triangle CED$。
再根据全等三角形的性质,全等三角形的对应角相等,所以$\angle1=\angle2$。
2. (2)证明$BC// DE$:
因为$AB = AC$,所以$\angle ABC=\angle ACB$。
由(1)知$\triangle BDE\cong\triangle CED$,所以$\angle BDE=\angle CED$。
设$\angle ABC = x$,$\angle BDE = y$,则$\angle AED=\angle ADE$(因为$AD = AE$,等腰三角形两底角相等)。
在$\triangle ADE$中,$\angle ADE=\frac{180^{\circ}-\angle A}{2}$,$\angle AED=\frac{180^{\circ}-\angle A}{2}$。
又因为$\angle AED=\angle EDC+\angle C$,$\angle ADE=\angle DEB+\angle B$(三角形外角性质:三角形的一个外角等于不相邻的两个内角之和),且$\angle B=\angle C$。
由$\angle1=\angle2$,可得$\angle EDC=\angle DEB$。
根据内错角相等,两直线平行,所以$BC// DE$。
综上,(1)已证$\angle1 = \angle2$;(2)已证$BC// DE$。
因为$\triangle ABE\cong\triangle ACD$,根据全等三角形的性质,全等三角形的对应边相等,对应角相等,所以$AB = AC$,$AD = AE$,$\angle B=\angle C$。
又因为$AB = AC$,$AD = AE$,所以$AB - AD=AC - AE$,即$BD = CE$。
在$\triangle BDE$和$\triangle CED$中:
$\left\{\begin{array}{l}BD = CE\\\angle B=\angle C\\BE = CD\end{array}\right.$(由$\triangle ABE\cong\triangle ACD$得$BE = CD$)。
根据$SAS$(边角边)判定定理,$\triangle BDE\cong\triangle CED$。
再根据全等三角形的性质,全等三角形的对应角相等,所以$\angle1=\angle2$。
2. (2)证明$BC// DE$:
因为$AB = AC$,所以$\angle ABC=\angle ACB$。
由(1)知$\triangle BDE\cong\triangle CED$,所以$\angle BDE=\angle CED$。
设$\angle ABC = x$,$\angle BDE = y$,则$\angle AED=\angle ADE$(因为$AD = AE$,等腰三角形两底角相等)。
在$\triangle ADE$中,$\angle ADE=\frac{180^{\circ}-\angle A}{2}$,$\angle AED=\frac{180^{\circ}-\angle A}{2}$。
又因为$\angle AED=\angle EDC+\angle C$,$\angle ADE=\angle DEB+\angle B$(三角形外角性质:三角形的一个外角等于不相邻的两个内角之和),且$\angle B=\angle C$。
由$\angle1=\angle2$,可得$\angle EDC=\angle DEB$。
根据内错角相等,两直线平行,所以$BC// DE$。
综上,(1)已证$\angle1 = \angle2$;(2)已证$BC// DE$。
查看更多完整答案,请扫码查看


