《2025年名师面对面学科素养评价九年级数学全一册浙教版》

1.一小球被抛出后，距离地面的高度$h$(米)和飞行时间$t$(秒)满足函数关系式$h = -5(t - 1)^2 + 6$，则小球距离地面的最大高度是 (C)

A.1 米
B.5 米
C.6 米
D.7 米

答案： 1.C

2. 如图，某广场有一喷水池，水从地面喷出，以水平地面为$x$轴，出水点为原点，建立平面直角坐标系，水在空中划出的曲线是抛物线$y = -x^2 + 4x$(单位：米)的一部分，则水喷出的最大高度是 (A)


A.4 米
B.3 米
C.2 米
D.1 米

答案： 2.A

3. 便民商店经营一种商品，在销售过程中，发现一周利润$y$(元)与每件销售价$x$(元)之间的关系满足$y = -2x^2 + 80x + 758$，由于某种原因，销售价不低于$15$元，不高于$22$元，那么一周可获得最大利润是 (B)

A.758 元
B.1 558 元
C.1 550 元
D.1 508 元

答案： 3.B

4. 汽车刹车后行驶的距离$s$(单位：米)关于行驶时间$t$(单位：秒)的函数表达式是$s = 15t - 6t^2$.则汽车从刹车到停止所用时间为1.25秒.

答案： 4.1.25

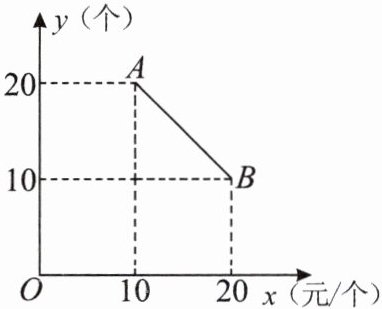
5. 某食品零售店新上架一款冷饮产品，每个成本为$8$元，在销售过程中，每天的销售量$y$(个)与销售价格$x$(元/个)的关系如图所示，当$10 \leq x \leq 20$时，其图象是线段$AB$.则该食品零售店每天销售这款冷饮产品的最大利润为121元(利润=总销售额—总成本).

答案： 5.121

6. 如图，一列火车$B$在$A$城的正北$240 km$处，以$120 km/h$的速度驶向$A$城.同时，一辆汽车$C$在$A$城的正东$120 km$处，以$120 km/h$的速度驶向正西方向行驶.假设火车和汽车的行驶的方向和速度都保持不变，问：何时火车与汽车之间的距离最近？最近距离是多少千米？当火车与汽车之间的距离最近时，汽车是否已过铁路与公路的交叉口？（两车长度忽略不计）

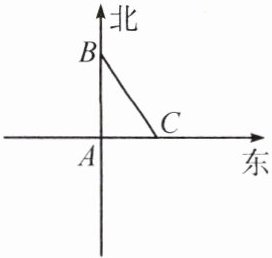
答案： 6.解：设两车经过的时间为$t(h)$，两车之间的距离为$y(km)$，
由题意得：$AB = 240 - 120t$，$AC = 120 - 120t$，
在$Rt\triangle ABC$中，$BC^{2}=AB^{2}+AC^{2}=(240 - 120t)^{2}+(120 -$
$120t)^{2}=28800(t - \frac{3}{2})^{2}+7200$，当$t = \frac{3}{2}$时，$BC$之间的距离
最小，此时$BC = \sqrt{7200}=60\sqrt{2}km$，
当$t = \frac{3}{2}$时，汽车运动的距离为$120×\frac{3}{2}=180km ＞ 120km$，
故已过铁路与公路的交叉口．
答：当经过$\frac{3}{2}$小时时汽车与火车的距离最近，最近距离为
$60\sqrt{2}km$，此时汽车已过铁路与公路的交叉口．