《2025年名师面对面学科素养评价九年级数学全一册浙教版》

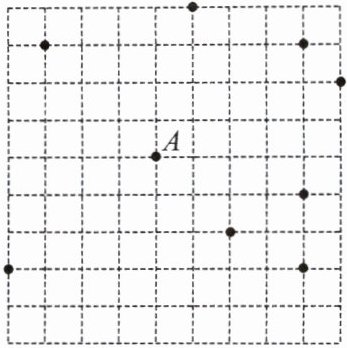
7.如图，在网格(每个小正方形的边长均为 1)中选取 9 个格点(各线的交点称为格点)，若以 A 为圆心，r 为半径画圆，选取的格点中除点 A 外恰好有 4 个在圆内，则 r 的取值范围为 (C)


A.$2\sqrt{2} ＜ x ＜ \sqrt{17}$
B.$\sqrt{17} ＜ x ＜ 3\sqrt{2}$
C.$3\sqrt{2} ＜ x \leq 5$
D.$5 ＜ x ＜ \sqrt{29}$

答案： 7.C

8.点 P 不在⊙O 上，若点 P 到⊙O 上的点的最小距离是 4 cm，最大距离是 9 cm，则⊙O 的半径是 $6.5 cm$或$2.5 cm$.

答案： 8.$6.5 cm$或$2.5 cm$

9.如图，BD，CE 是△ABC 的高，M 为 BC 的中点.试说明点 B，C，D，E 在以点 M 为圆心的同一个圆上.

答案：
9.证明:连结$ME$，$MD$，$\because BD$，$CE$分别是$\triangle ABC$的高，$M$为$BC$的中点，$\therefore ME = MD = MC = MB = \frac{1}{2}BC$，

$\therefore$点$B$，$C$，$D$，$E$在以点$M$为圆心的同一圆上.

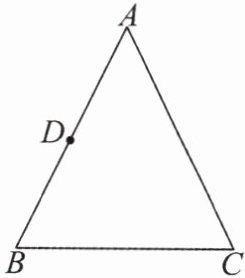
10.如图，在△ABC 中，AB = AC = $2\sqrt{5}$，BC = 4，D 是 AB 的中点.若以点 D 为圆心，r 为半径作⊙D，使点 B 在⊙D 内，点 C 在⊙D 外.试求 r 的取值范围.

答案：
10.解:连结$CD$，过点$A$作$AE \perp BC$于点$E$.
过点$D$作$DF \perp BC$于点$F$，显然$DF // AE$，
$\because AB = AC = 2\sqrt{5}$，$BC = 4$，
$\therefore BE = \frac{1}{2}BC = 2$，$\therefore AE = 4$，
$\because DF$是中位线，
$\therefore DF = \frac{1}{2}AE = 2$，$BF = \frac{1}{2}BE = 1$，

$\therefore CF = 3$，$\therefore CD = \sqrt{13}$，
又$DB = \frac{1}{2}AB = \sqrt{5}$，$\therefore r$的取值范围是$\sqrt{5} ＜ r ＜ \sqrt{13}$.