第24页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
1.学习圆的性质后,小铭与小熹就讨论起来,小铭说:“被直径平分的弦也与直径垂直.”小熹说:“用反例就能说明这是假命题.”下列判断正确的是
(
A.两人说的都对
B.小铭说的对,小熹说的反例不存在
C.两人说的都不对
D.小铭说的不对,小熹说的反例存在
(
D
)A.两人说的都对
B.小铭说的对,小熹说的反例不存在
C.两人说的都不对
D.小铭说的不对,小熹说的反例存在
答案:
1.D
2.如图,$\odot O$的直径$AB$与弦$CD($不是直径)交于点$E$,且$CE = DE$,$\angle A = 30^{\circ}$,$OC = 4$,那么$CD$的长为
(
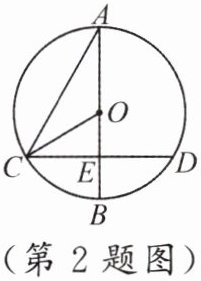
A.$2\sqrt{3}$
B.$4$
C.$4\sqrt{3}$
D.$8$
(
C
)
A.$2\sqrt{3}$
B.$4$
C.$4\sqrt{3}$
D.$8$
答案:
2.C
3.如图,$AB$是$\odot O$的弦,$C$是$\overset{\frown}{AB}$的中点,$OC$交$AB$于点$D$.若$AB = 8\ {cm}$,$CD = 2\ {cm}$,则$\odot O$的半径为

5
$\ {cm}$.
答案:
3.5
4.如图,已知$C$是优弧$AB$的中点.若$\angle AOC = 4\angle B$,$OC = 4$,则$AB =$
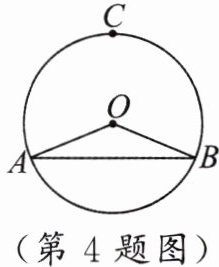
$4\sqrt{3}$
.
答案:
4.$4\sqrt{3}$
5.$AB$是$\odot O$的弦,$OM \perp AB$,垂足为$M$,连结$OA$.若$\triangle AOM$中有一个角是$30^{\circ}$,$OM = 2\sqrt{3}$,则弦$AB$的长为
12或4
.
答案:
5.12或4
6.下右图是一个隧道的横截面,它的形状是以点$O$为圆心的圆的一部分.如果$M$是$\odot O$中弦$CD$的中点,$EM$经过圆心$O$交$\odot O$于点$E$,并且$CD = 4$,$EM = 6$,求$\odot O$的半径.
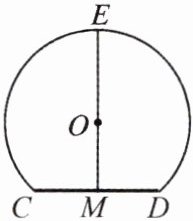

答案:
6.解:连结OC,设圆的半径是x,
在Rt△COM中,有OC²=CM²+OM²,
 即:x²=2²+(6−x)²,解得:x=$\frac{10}{3}$,
即:x²=2²+(6−x)²,解得:x=$\frac{10}{3}$,
所以圆的半径长是$\frac{10}{3}$.
6.解:连结OC,设圆的半径是x,
在Rt△COM中,有OC²=CM²+OM²,
 即:x²=2²+(6−x)²,解得:x=$\frac{10}{3}$,
即:x²=2²+(6−x)²,解得:x=$\frac{10}{3}$,所以圆的半径长是$\frac{10}{3}$.
查看更多完整答案,请扫码查看


