《2025年名师面对面学科素养评价九年级数学全一册浙教版》

6.在同一直角坐标系中，$a \neq 0$，函数$y = ax$与$y = ax^{2}$的图象可能正确的有 (C)


A.0 个
B.1 个
C.2 个
D.3 个

答案： 6.C

7.如图所示，桥拱是抛物线形，其函数表达式为$y = -\frac{1}{4}x^{2}$，设正常水位时，水面宽$AB$为$12\ m$，桥下水深为$2\ m$.
(1)正常水位时，求水面离桥拱顶部的距离是多少米?
(2)为保证过往船只顺利航行，桥下水面宽度应不小于$8\ m$.问：水深超过多少米时会影响过往船只顺利航行?

答案： 7.解：
(1)因为AB=12m，所以设点B坐标为(6,y)，代入函数表达式$y=-\frac{1}{4}x^{2}$得y=-9，所以水面离桥拱顶部的距离为9m。
(2)当桥下水面宽度为8m时，设此时点B坐标为(4,y)，代入函数表达式$y=-\frac{1}{4}x^{2}，$得y=-4，
所以水面离桥拱顶部的距离为4m，
而桥拱顶部到水底距离为9+2=11(m)，所以11-4=7(m)，
即水深超过7m时会影响过往船只顺利航行。

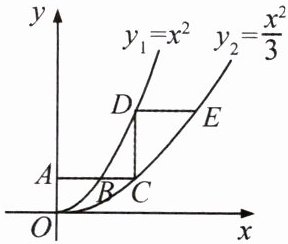
8.如图，平行于$x$轴的直线$AC$分别交函数$y_{1} = x^{2}(x \geqslant 0)$与$y_{2} = \frac{x^{2}}{3}(x \geqslant 0)$的图象于$B$，$C$两点，过点$C$作$y$轴的平行线交$y_{1}$的图象于点$D$，直线$DE // AC$，交$y_{2}$的图象于点$E$.求$\frac{DE}{AB}$的值.

答案： 8.解：设A点坐标为(0,a)(a＞0)。令$x^{2}=a，$
解得$x=\pm\sqrt{a}，$$\therefore$点B的坐标为$(\sqrt{a},a)。$
令$\frac{x^{2}}{3}=a，$则$x=\pm\sqrt{3a}，$$\therefore$点C的坐标为$(\sqrt{3a},a)。$
$\because CD// y$轴，$\therefore$点D的横坐标与点C的横坐标相同，为$\sqrt{3a}，$
$\therefore y_{D}=(\sqrt{3a})^{2}=3a，$$\therefore$点D的坐标为$(\sqrt{3a},3a)。$
$\because DE// AC，$$\therefore$点E的纵坐标为3a，令$\frac{x^{2}}{3}=3a，$
$\therefore x=\pm3\sqrt{a}，$
$\therefore$点E的坐标为$(3\sqrt{a},3a)，$$\therefore DE=3\sqrt{a}-\sqrt{3a}，$
$\therefore\frac{DE}{AB}=\frac{3\sqrt{a}-\sqrt{3a}}{\sqrt{a}}=3-\sqrt{3}。$