《2025年名师面对面学科素养评价九年级数学全一册浙教版》

1.神奇的自然界处处蕴含着数学知识.动物学家在鹦鹉螺外壳上发现，其每圈螺纹的直径与相邻螺纹直径的比约为 0.618.这体现了数学中的 (D)

A.平移
B.旋转
C.轴对称
D.黄金分割

答案： 1.D

2.已知线段$a$，$b$，$c$，其中$c$是$a$和$b$的比例中项，$a = 4$，$b = 9$，则$c$等于 (B)

A.4
B.6
C.9
D.36

答案： 2.B

3.在设计人体雕像时，使雕像上部(腰部以上)与下部(腰部以下)的高度比，等于下部与全部的高度比，可以增加视觉美感.如图，按此比例设计一座高度为 2 m 的雷锋雕像，那么该雕像的下部设计高度约是(结果精确到 0.01 m，参考数据：$\sqrt{2} \approx 1.414$，$\sqrt{3} \approx 1.732$，$\sqrt{5} \approx 2.236$) (B)

A.0.73 m
B.1.24 m
C.1.37 m
D.1.42 m

答案： 3.B

4.一本书的宽与长之比为黄金比，书的宽为 14 cm，则它的长为 (A)

A.$(7\sqrt{5} + 7) cm$
B.$(21 - 7\sqrt{5}) cm$
C.$(7\sqrt{5} - 7) cm$
D.$(7\sqrt{5} - 21) cm$

答案： 4.A

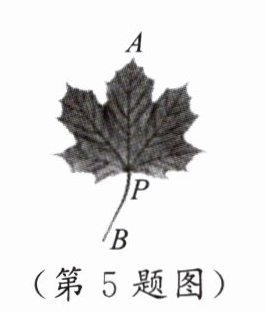
5.大自然是美的设计师，即使是一片小小的树叶，也蕴含着“黄金分割”.如图，$P$为$AB$的黄金分割点($AP ＞ PB$)，如果$AB$的长度为 8 cm，那么$AP$的长度为 $(4\sqrt{5}-4)$ cm.

答案： $5.(4\sqrt{5}-4)$

6.(1)已知$a = 4$，$c = 9$，若$b$是$a$，$c$的比例中项，求$b$的值.
(2)已知线段$MN$是$AB$，$CD$的比例中项，$AB = 4 cm$，$CD = 5 cm$，求$MN$的长，并思考两题有何区别.

答案： 解：
(1)
∵b 是 a，c 的比例中项，
∴a:b = b:c，
∴$b^{2}=ac$
∴$b = \pm \sqrt{ac}，$
∵a = 4，c = 9，
∴$b = \pm \sqrt{36} = \pm 6，$即$ b = \pm 6。$
(2)
∵MN 是线段，
∴MN＞0；
∵线段 MN 是 AB，CD 的比例中项，
∴AB:MN = MN:CD，
∴$MN^{2}=AB·CD。$
∴$MN = \pm \sqrt{AB·CD}$
∵AB = 4 cm，
CD = 5 cm，
∴$MN = \pm \sqrt{20} = \pm 2\sqrt{5}，$
MN 不可能为负值，则$ MN = 2\sqrt{5}。$
通过解答
(1)
(2)发现，b，MN 同时作为比例中项出现，b 可以取负值，而 MN 不可以取负值。