《2025年名师面对面学科素养评价九年级数学全一册浙教版》

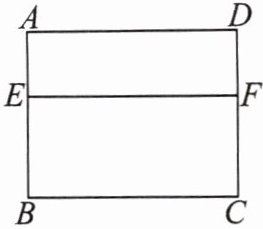
7.在 20 世纪 70 年代，我国著名数学家华罗庚教授将黄金分割法作为一种“优选法”，在全国大规模推广，取得了很大成果.如图，利用黄金分割法，所作$EF$将矩形窗框$ABCD$分为上下两部分，其中$E$为边$AB$的黄金分割点，即$BE^{2} = AE · AB$.已知$AB$为 2 米，则线段$BE$的长为 $\sqrt{5}-1$ 米.

答案： $7.\sqrt{5}-1$

8.如图，乐器上的一根弦$AB = 80 cm$，两个端点$A$，$B$固定在乐器板面上.支撑点$C$是靠近点$B$的黄金分割点，支撑点$D$是靠近点$A$的黄金分割点.求$C$，$D$之间的距离.(结果保留根号)

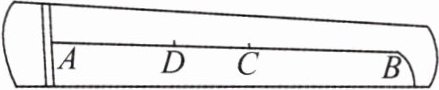
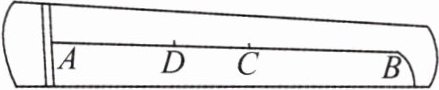
答案： 解：
∵点 C 是靠近点 B 的黄金分割点，
点 D 是靠近点 A 的黄金分割点，
∴$AC = BD = 80× \frac{\sqrt{5}-1}{2}=40\sqrt{5}-40。$
∴$CD = AC + BD - AB = 2BD - AB = 80\sqrt{5}-160。$
答：C，D 之间的距离为$(80\sqrt{5}-160)cm。$

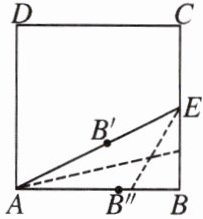
9.如图，用纸折出黄金分割点：裁一张正方形的纸片$ABCD$，先折出$BC$的中点$E$，再折出线段$AE$，然后通过折叠使$EB$落在线段$EA$上，折出点$B$的新位置$B'$，因而$EB' = EB$.类似地，在$AB$上折出点$B''$，使$AB'' = AB'$.这时$B''$就是$AB$的黄金分割点.请你证明这个结论.

答案： 证明：设正方形 ABCD 的边长为 2.
∵E 为 BC 的中点，
∴BE = 1，
∴$AE = \sqrt{AB^{2}+BE^{2}}=\sqrt{5}。$
又
∵B'E = BE = 1，
∴$AB' = AE - B'E = \sqrt{5}-1。$
又
∵$AB'' = AB' = \sqrt{5}-1，$
∴$AB'':AB = (\sqrt{5}-1):2，$
∴B''是线段 AB 的黄金分割点。