《2025年名师面对面学科素养评价九年级数学全一册浙教版》

三、相似三角形的应用
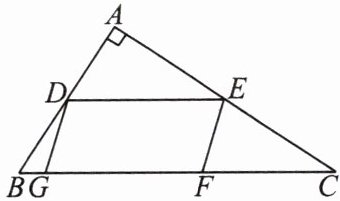
【例 3】如图，有一块形状为$Rt \bigtriangleup ABC$的斜板余料.已知$\angle A = 90^{\circ}$，$AB = 6 cm$，$AC = 8 cm$.要把它加工成一个形状为$□ DEFG$的工件，使$GF$在$BC$上，$D$，$E$两点分别在$AB$，$AC$上，且$DE = 5 cm$，求工件$□ DEFG$的面积.

答案：
解:过点$A$作$AM \perp BC$，交$DE$于点$N$，可求得$AM = 4.8(cm)$，

∵四边形$DEFG$是平行四边形，
∴$DE // BC,DE = FG = 5cm$，
∴$\triangle ADE \backsim \triangle ABC$，$\frac{DE}{BC} = \frac{AN}{AM} = \frac{1}{2}$，
∴$AN = MN = 2.4cm$，
∴$□ DEFG$的面积为$5 × 2.4 = 12(cm^{2})$.

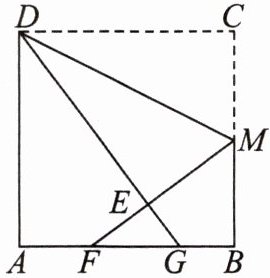
练习3如图，折叠边长为$4$的正方形纸片$ABCD$，折痕是$DM$，点$C$落在点$E$处.分别延长$ME$，$DE$交$AB$于点$F$，$G$，若点$M$是边$BC$的中点，则$FG =$$\frac{5}{3}$.

答案： 练习3.$\frac{5}{3}$ [解析]连结$DF$，可证得$Rt \triangle DAF \cong Rt \triangle DEF$(HL)，则$AF = EF$，设$AF = x cm$，则$EF = x cm$，在$\triangle FBM$中，利用勾股定理求得$x = \frac{4}{3}$，再由$\triangle FGE \backsim \triangle FMB$，即可求得答案.

四、相似多边形
【例 4】根据中国人民政治协商会议第一届全体会议主席团 1949 年 9 月 28 日公布的国旗制法说明，我国五种规格的国旗旗面为相似矩形.已知一号国旗的标准尺寸是长$288 cm$，高$192 cm$，则下图矩形尺寸不符合标准的是
(B)


A.$160 cm$
B.$120 cm$
C.$96 cm$
D.$64 cm$

答案： 【例 4】B

练习4如图，菱形$ABCD$与菱形$AEFG$相似.菱形$AEFG$的顶点$G$在菱形$ABCD$的边$BC$上运动，$GF$与$AB$相交于点$H$，$\angle E = 60^{\circ}$.若$CG = 3$，$AH = 7$，则菱形$ABCD$的边长为9.

答案： 练习4.9 [解析]连结$AC$，首先证明$\triangle ABC$是等边三角形，再证明$\triangle BGH \backsim \triangle CAG$，推出$\frac{BG}{AC} = \frac{BH}{CG}$，由此构建方程即可解决问题.