第22页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
1.下列运动形式属于旋转的是 (
A.在空中上升的氢气球
B.飞驰的火车
C.时钟上钟摆的摆动
D.运动员掷出的标枪
C
)A.在空中上升的氢气球
B.飞驰的火车
C.时钟上钟摆的摆动
D.运动员掷出的标枪
答案:
1.C
2.如图,线段$OA$在平面直角坐标系内,$A$点坐标为$(2,5)$,线段$OA$绕原点$O$逆时针旋转$90^{\circ}$,得到线段$OA^{\prime}$,则点$A^{\prime}$的坐标为 (
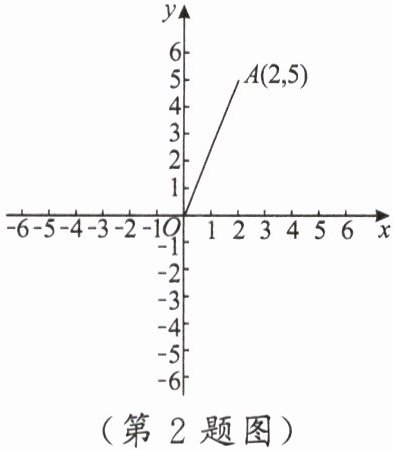
A.$(-5,2)$
B.$(5,2)$
C.$(2,-5)$
D.$(5,-2)$
A
)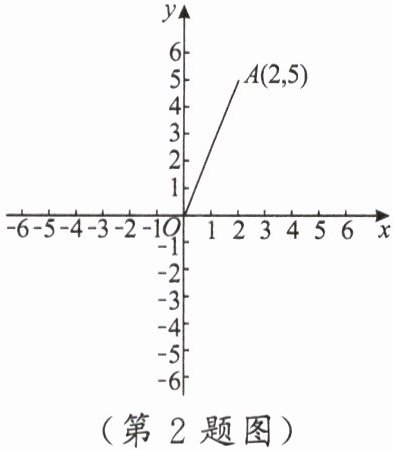
A.$(-5,2)$
B.$(5,2)$
C.$(2,-5)$
D.$(5,-2)$
答案:
2.A
3.如图,在$ Rt\triangle ABC$中,$\angle ACB = 90^{\circ}$,$\angle A = 30^{\circ}$,$BC = 2$,将$\triangle ABC$绕点$C$顺时针旋转得到$\triangle A^{\prime}B^{\prime}C$,其中点$A^{\prime}$与点$A$是对应点,点$B^{\prime}$与点$B$是对应点.若点$B^{\prime}$恰好落在边$AB$上,则点$A$到直线$A^{\prime}C$的距离等于 (
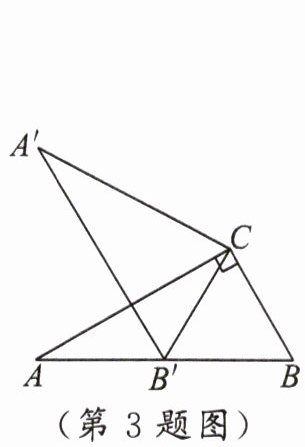
A.$3\sqrt{3}$
B.$2\sqrt{3}$
C.$3$
D.$2$
C
)
A.$3\sqrt{3}$
B.$2\sqrt{3}$
C.$3$
D.$2$
答案:
3.C
4.如图,将$\triangle ABC$绕点$A$逆时针旋转角$\alpha(0^{\circ}<\alpha<180^{\circ})$得到$\triangle ADE$,点$B$的对应点$D$恰好落在边$BC$上.若$DE\perp AC$,$\angle CAD = 25^{\circ}$,则旋转角$\alpha$的度数是
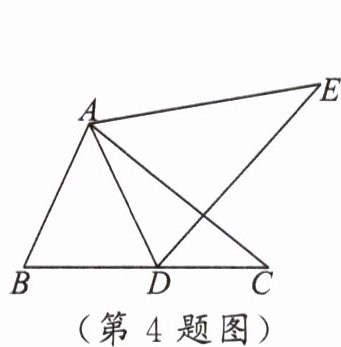
50°
.
答案:
4.50°
5.一个正方形绕着它的中心旋转一定角度后,就能与它自身重合,这个角度至少是
90
.
答案:
5.90
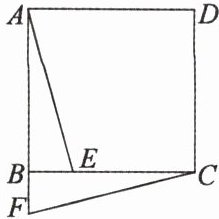
6.如图,在正方形$ABCD$中,$E$为边$BC$上的一点,将$\triangle ABE$旋转后得到$\triangle CBF$.
(1)指出旋转中心及旋转的角度.
(2)判断$AE$与$CF$的位置关系.
(3)如果正方形的面积是$18\ cm^2$,$\triangle BCF$的面积是$5\ cm^2$,问四边形$AECD$的面积是多少?
(1)指出旋转中心及旋转的角度.
(2)判断$AE$与$CF$的位置关系.
(3)如果正方形的面积是$18\ cm^2$,$\triangle BCF$的面积是$5\ cm^2$,问四边形$AECD$的面积是多少?

答案:
6.解:
(1)旋转中心是B,旋转角度是90°.
(2)延长AE交CF于点M.
∵△ABE≌△CBF,
∴AE=CF,∠EAB=∠BCF.
又
∵∠AEB=∠CEM,∠ABE=90°,
∴∠ECM+∠CEM=90°,
∴AE⊥CF.
(3)
∵△ABE≌△CBF,
∴△ABE的面积是5cm²,
∴四边形AECD的面积是18−5=13cm².
(1)旋转中心是B,旋转角度是90°.
(2)延长AE交CF于点M.
∵△ABE≌△CBF,
∴AE=CF,∠EAB=∠BCF.
又
∵∠AEB=∠CEM,∠ABE=90°,
∴∠ECM+∠CEM=90°,
∴AE⊥CF.
(3)
∵△ABE≌△CBF,
∴△ABE的面积是5cm²,
∴四边形AECD的面积是18−5=13cm².
查看更多完整答案,请扫码查看


