《2025年名师面对面学科素养评价九年级数学全一册浙教版》

7.在⊙O 中，若弦 BC 垂直平分半径 OA，则弦 BC 所对的圆周角等于60°或120°.

答案： 7.60°或120°

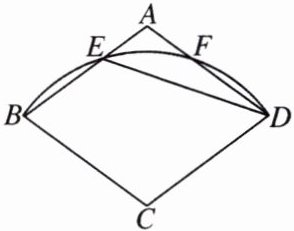
8.如图，在菱形 ABCD 中，以点 C 为圆心、CB 长为半径作$\overset{\frown}{BD}$，与 AB，AD 分别交于点 E，F，点 E，F 恰好是$\overset{\frown}{BD}$的三等分点，连结 DE，则∠AED = 54°.

答案： 8.54° [解析]连结BD,设∠BDE的度数为x，
∵点E，F恰好是BD的三等分点，
∴∠EBD=2x,
　∠BCD=6x,
∵CB=CD,
∴∠CBD=∠CDB=90°−3x,
　易证∠ABD=∠CDB，即2x=90°−3x,解得x=18°，
∴∠AED=∠EBD+∠BDE=2x+x=3x=54°.

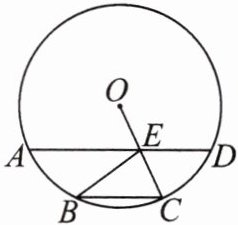
9.如图，已知在⊙O 中，$\overset{\frown}{AB}=\overset{\frown}{BC}=\overset{\frown}{CD}$，OC 与 AD 相交于点 E.求证：
(1)AD//BC.
(2)四边形 BCDE 为菱形.

答案：
9.解:
(1)连结BD，
∵AB = BC = CD，
∴∠ADB=∠CBD,
∴AD//BC.
　　　　　　　　　　　　　　　　　　　　
(2)连结CD,BD交OC于点F，
∵AD//BC,
∴∠EDF=∠CBF,
∵BC=CD,
∴BC=CD,
∴BF=DF,
　又∠DFE=∠BFC,
∴△DEF≌△BCF(ASA),
∴DE=BC,
∴四边形BCDE是平行四边形，
　又BC=CD,
∴四边形BCDE是菱形.

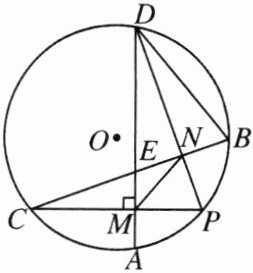
10.如图，在⊙O 中，P 为$\overset{\frown}{AB}$的中点，弦 AD，PC 互相垂直，垂足为 M，BC 分别与 AD，PD 相交于点 E，N，连结 BD，MN.
(1)求证：N 为 BE 的中点.
(2)若⊙O 的半径为 8，$\overset{\frown}{AB}$的度数为 90°，求线段 MN 的长.

答案：
10.
(1)证明:
∵AD⊥PC,
∴∠EMC=90°,
∵点P为AB的中点，
∴PA=PB,
∴∠ADP=∠BCP,
　　　　　　　　　　　　　　　　　　　　
∵∠CEM=∠DEN,
∴∠DNE=∠EMC=90°=∠DNB,
∵PA=PB,
∴∠BDP=∠ADP,
∴∠DEN=∠DBN,
∴DE=DB,
∴EN=BN,
∴N为BE的中点.
(2)解:连结OA,OB,AB,AC,
∵AB的度数为90°,
∴∠AOB=90°,
∵OA=OB=8,
∴AB=8$\sqrt{2}$,
　由
(1)同理得:AM=EM,
∵EN=BN,
∴MN是△AEB的中位线，
∴MN=$\frac{1}{2}$AB=4$\sqrt{2}$.