《2025年名师面对面学科素养评价九年级数学全一册浙教版》

7. 在平面直角坐标系中，点 A 的坐标为(3,4)，以点 A 为圆心、5 为半径的圆与直线 y = -x 的位置关系是
(C)

A.相离
B.相切
C.相交
D.以上都有可能

答案： 7.C

8. 如图，Rt△ABC 中，∠ACB = 90°，AC = 8，AB = 10.P 是 AC 上的动点(P 不与 A，C 重合)，设 PC = x，点 P 到 AB 的距离为 y.
(1)求 y 与 x 的函数表达式.
(2)试讨论以 P 为圆心，半径长为 x 的圆与 AB 所在直线的位置关系，并指出相应的 x 的取值范围.

答案：
8.解:
(1)作PH⊥AB于H,如图，在Rt△ABC中，
　　　　　　　　　　
$BC = \sqrt{10^{2} - 8^{2}} = 6，$PC = x，PH = y，则PA = 8 - x，
∵∠PAH = ∠BAC，
∴Rt△APH∽Rt△ABC，
∴$\frac{PH}{BC} = \frac{AP}{AB}，$即$\frac{y}{6} = \frac{8 - x}{10}，$
∴$y = -\frac{3}{5}x + \frac{24}{5}(0 ＜ x ＜ 8).$
(2)当PH = PC时，⊙P与直线相切，
即$-\frac{3}{5}x + \frac{24}{5} = x，$解得x = 3；
当PH ＜ PC时，⊙P与直线相交，
即$-\frac{3}{5}x + \frac{24}{5} $＜ x，解得x ＞ 3；
当PH ＞ PC时，⊙P与直线相离，
即$-\frac{3}{5}x + \frac{24}{5} ＞ x，$解得x ＜ 3；
所以当0 ＜ x ＜ 3时，⊙P与AB所在直线相离;当x = 3时，⊙P与AB所在直线相切;当3 ＜ x ＜ 8时，⊙P与AB所在直线相交.

9. 点 P 是平面直角坐标系中第一象限上的一点，过点 P 向 x 轴，y 轴作垂线段，若垂线段的长度的和为 4，则点 P 叫作“垂距点”.例如：下图中的 P(1,3)是“垂距点”.
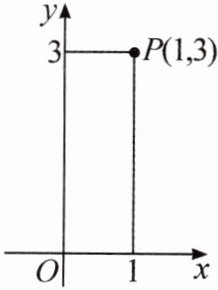
(1)在点 A(2,2)，B($\frac{3}{2}$,$\frac{5}{2}$)，C(4,4)中，是“垂距点”的点为A,B.
(2)⊙T 的圆心 T 的坐标为(1,0)，半径为 r.若⊙T 上存在“垂距点”，求 r 的取值范围.

答案：
9.解:
(1)A,B.
(3)设点P坐标为(x,y)，
∵x ＞ 0,y ＞ 0时,x + y = 4,
即y = -x + 4(0 ＜ x ＜ 4);画出该函数图象，如图所示.
　　　　　　　　
过点T作TN⊥直线DE于点N，
易证△DNT为等腰直角三角形，
∴$TN = \frac{\sqrt{2}}{2}TD = \frac{\sqrt{2}}{2}×$|4 - 1|$ = \frac{3\sqrt{2}}{2}；$
当⊙T过点E(0，4)时，⊙T上不存在“垂距点”，
∴若⊙T上存在“垂距点”，则r的取值范围是$\frac{3\sqrt{2}}{2}≤r ＜ 4.$