《2025年名师面对面学科素养评价九年级数学全一册浙教版》

1.在$-2$，$-1$，$1$，$2$这四个数中随机取出一个数，其倒数等于本身的概率是$\frac{1}{2}$.

答案： 1.$\frac{1}{2}$

2.有三张正面分别写有数字$-2$，$-1$，$1$的卡片，它们的背面完全相同.将这三张卡片背面朝上洗匀后随机抽取一张，以其正面数字作为$x$的值，放回卡片洗匀，再从三张卡片中随机抽取一张，以其正面数字作为$y$的值，两次结果记作$(x,y)$.
(1)用画树状图或列表的方法表示$(x,y)$所有可能出现的结果.
(2)求使分式$\frac{x^{2}-3xy}{x^{2}-y^{2}}+\frac{y}{x - y}$有意义的$(x,y)$出现的概率.

答案： 2.解:
(1)所有可能结果为$(-2,-2),(-2,-1),(-2,1),(-1,-2),(-1,-1),(-1,1),(1,-2),(1,-1),(1,1)$.
(2)要使分式$\frac{x^2 - 3xy}{x^2 - y^2} + \frac{y}{x - y}$有意义，
　则有$(x + y)(x - y) \neq 0$，
　$\therefore$只有$(-2,-1),(-2,1),(-1,-2),(1,-2)$符合条件，$\therefore$使分式$\frac{x^2 - 3xy}{x^2 - y^2} + \frac{y}{x - y}$有意义的$(x,y)$出现的概率为$\frac{4}{9}$.

3.一只蚂蚁在如图所示的七巧板上任意爬行，已知它停在这副七巧板上的任何一点的可能性都相同，那么它停在$1$号板上的概率是$\frac{1}{4}$.

答案： 3.$\frac{1}{4}$

4.如图，在方格纸中，$\triangle ABC$的三个顶点及$D$，$E$，$F$，$G$，$H$五个点分别位于小正方形的顶点上.
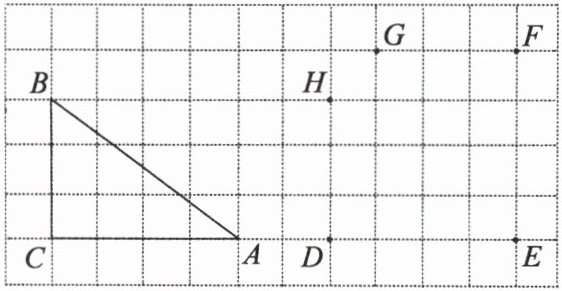
(1)现以$D$，$E$，$F$，$G$，$H$中的三个点为顶点画三角形，在所画的三角形中与$\triangle ABC$不全等但面积相等的三角形是$\triangle DFG$或$\triangle DHF$.(只需要填一个三角形)
(2)先从$D$，$E$两个点中任意取一个点，再从$F$，$G$，$H$三个点中任意取两个不同的点，以所取的这三个点为顶点画三角形，求所画三角形与$\triangle ABC$面积相等的概率.(用画树状图或列表法求解)

答案： 4.解:
(1)$\triangle DFG$或$\triangle DHF$.
(2)画树状图略，共有6种等可能结果，其中与$\triangle ABC$面积相等的有3种，即$\triangle DHF$，$\triangle DGF$和$\triangle EGF$，所以所画三角形与$\triangle ABC$面积相等的概率为$P = \frac{1}{2}$.