《2025年名师面对面学科素养评价九年级数学全一册浙教版》

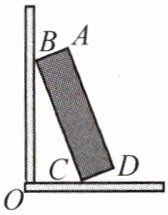
7.如图，一块矩形木板 $ABCD$ 斜靠在墙边($OC \perp OB$，点 $A$，$B$，$C$，$D$，$O$ 在同一平面内)，已知 $AB = a$，$AD = b$，$\angle BCO = x$，则点 $A$ 到 $OC$ 的距离为 (D)


A.$a \sin x + b \sin x$
B.$a \cos x + b \cos x$
C.$a \sin x + b \cos x$
D.$a \cos x + b \sin x$

答案： 7.D

8.小华将一张纸对折后做成的纸飞机如图 1 所示.纸飞机机尾的横截面是一个轴对称图形，其示意图如图 2 所示.已知 $AD = BE = 10 cm$，$CD = CE = 5 cm$，$AD \perp CD$，$BE \perp CE$，$\angle DCE = 40°$.(结果精确到 $0.1 cm$，参考数据：$\sin 20° \approx 0.34$，$\cos 20° \approx 0.94$，$\tan 20° \approx 0.36$，$\sin 40° \approx 0.64$，$\cos 40° \approx 0.77$，$\tan 40° \approx 0.84$)

(1)连结 $DE$，求线段 $DE$ 的长.
(2)求点 $A$，$B$ 之间的距离.

答案：
8.
(1)解:如图，过点C作CF ⊥ DE于点F，
　　　　　　　
　DF = CD · sin20° ≈ 5 × 0.34 = 1.7,
∴DE = 2DF = 3.4cm。
(2)解:如图，连结AB.设纸飞机机尾的横截面的对称轴为直线l，
　
　则AB ⊥ l,DE ⊥ l,
∴AB // DE.过点D作DG ⊥ AB于点G，过点E作EH ⊥ AB于点H，易证四边形DGHE是矩形，
∴DE = HG,
∴DG // l,EH // l，
∴∠GDC = ∠CEH = $\frac{1}{2}$∠DCE = 20°，
∵AD ⊥ CD,BE ⊥ CE,
∴∠DAB = ∠GDC = 20°，
　∠EBH = ∠CEH = 20°，
∴AG = AD · cos20° ≈ 10 × 0.94 = 9.4，
　BH = BE · cos20° ≈ 10 × 0.94 = 9.4，
∴AB = BH + AG + DE = 22.2cm。

9.探究：已知如图 1，在 $\triangle ABC$ 中，$\angle A = \alpha$ ($0° ＜ \alpha ＜ 90°$)，$AB = c$，$AC = b$，试用含 $b$，$c$，$\alpha$ 的式子表示 $\triangle ABC$ 的面积.
应用：如图 2，在 $□ ABCD$ 中，对角线 $AC$，$BD$ 相交成的锐角为 $\alpha$，若 $AC = a$，$BD = b$，试用含 $\alpha$，$b$，$\alpha$ 的式子表示 $□ ABCD$ 的面积.

答案：
9.解:探究:过点B作BD ⊥ AC，垂足为D.
∵AB = c,∠A = α，
　　　　　　　　　　　　　　　　　
∴BD = c · sinα，
∴S_{△ABC} = $\frac{1}{2}$AC · BD = $\frac{1}{2}$bc sinα。
　应用:由探究易知:S_{△DOC} = $\frac{1}{2}$ · OD · OC · sinα，
　而OC = $\frac{1}{2}$AC = $\frac{1}{2}$a,OD = $\frac{1}{2}$BD = $\frac{1}{2}$b，
∴S_{△DOC} = $\frac{1}{8}$ab sinα,S_{▱ABCD} = 4S_{△DOC} = $\frac{1}{2}$ab sinα。