第17页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
7.某人把 50 粒黄豆染色后与一袋黄豆充分混匀,接着抓出 100 粒黄豆,数出其中有 10 粒黄豆被染色,则这袋黄豆原来约有 (
A.10 粒
B.160 粒
C.450 粒
D.500 粒
C
)A.10 粒
B.160 粒
C.450 粒
D.500 粒
答案:
7.C
8.小明在操场上做游戏,他发现地上有一个不规则的封闭图形 ABC.为了知道它的面积,小明在封闭图形内划出了一个半径为 1 米的圆,在不远处向圈内掷石子,且记录如下:

请依此估计此封闭图形 ABC 的面积.
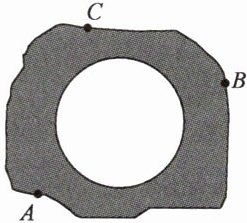

请依此估计此封闭图形 ABC 的面积.

答案:
8.解:由已知得:当分别投掷50次,150次,300次时,石子落在⊙O内(含⊙O上)的次数m与石子落在阴影内的次数n的比值分别是:$\frac{14}{19}$≈0.737,$\frac{43}{85}$≈0.506,$\frac{93}{186}$=0.5,
∴圆的面积大约是阴影部分面积的一半,
∵圆的面积大约是π×1²=π(m²),
∴阴影部分的面积大约是2π(m²).
∴封闭图形ABC的面积大约是π+2π=3π(m²).
∴圆的面积大约是阴影部分面积的一半,
∵圆的面积大约是π×1²=π(m²),
∴阴影部分的面积大约是2π(m²).
∴封闭图形ABC的面积大约是π+2π=3π(m²).
9.一个不透明的袋子中装有 4 个质地、大小均相同的小球,这些小球分别标有 3,4,5,x.
甲、乙两人每次同时从袋中各随机摸出 1 个小球,并计算摸出的这 2 个小球上数字之和,记录后都将小球放回袋中搅匀,进行重复试验,试验数据如表:

解答下列问题:
(1)如果试验继续进行下去,根据上表数据,出现“和为 8”的频率将稳定在它的概率附近,估计出现“和为 8”的概率是
(2)如果摸出的这两个小球上数字之和为 9 的概率是$\frac{1}{3}$,那么 x 的值可以取 7 吗?请用列表法或画树状图法说明理由.如果 x 的值不可以取 7,请写出一个符合要求的 x 值.
甲、乙两人每次同时从袋中各随机摸出 1 个小球,并计算摸出的这 2 个小球上数字之和,记录后都将小球放回袋中搅匀,进行重复试验,试验数据如表:

解答下列问题:
(1)如果试验继续进行下去,根据上表数据,出现“和为 8”的频率将稳定在它的概率附近,估计出现“和为 8”的概率是
0.33
.(2)如果摸出的这两个小球上数字之和为 9 的概率是$\frac{1}{3}$,那么 x 的值可以取 7 吗?请用列表法或画树状图法说明理由.如果 x 的值不可以取 7,请写出一个符合要求的 x 值.
答案:
9.解:
(1)0.33.
(2)不可以取7.
∵当x=7时,列树状图如下:

数字和7 8 10 7 9 11 8 9 12 10 11 12
∴P(两个小球上数字之和为9的概率)=$\frac{2}{12}$=$\frac{1}{6}$≠$\frac{1}{3}$,结合题目“和为8”的概率为$\frac{1}{3}$,得当x=4或5时,两个小球上数字之和为9的概率是$\frac{1}{3}$.
9.解:
(1)0.33.
(2)不可以取7.
∵当x=7时,列树状图如下:

数字和7 8 10 7 9 11 8 9 12 10 11 12
∴P(两个小球上数字之和为9的概率)=$\frac{2}{12}$=$\frac{1}{6}$≠$\frac{1}{3}$,结合题目“和为8”的概率为$\frac{1}{3}$,得当x=4或5时,两个小球上数字之和为9的概率是$\frac{1}{3}$.
查看更多完整答案,请扫码查看


