《2025年名师面对面学科素养评价九年级数学全一册浙教版》

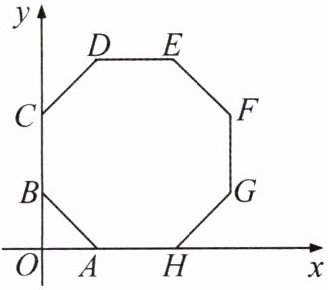
8. 如图所示，在平面直角坐标系中，多边形$ABCDEFGH$是正八边形，点$A$的坐标为$(2,0)$，点$B$的坐标为$(0,2)$.求点$E$的坐标.

答案： 8.解:延长ED交y轴于点K，连结OE，
∵点A的坐标为(2,0)，点B的坐标为(0,2)，
∴AB= $\sqrt{OA² + OB²}$ = $\sqrt{2² + 2²}$ = 2$\sqrt{2}$,
∴OK=2OB+BC=2×2+2$\sqrt{2}$=4+2$\sqrt{2}$,
　EK=KD + DE=2+2$\sqrt{2}$,
∴E点坐标为(2+2$\sqrt{2}$,4+2$\sqrt{2}$).

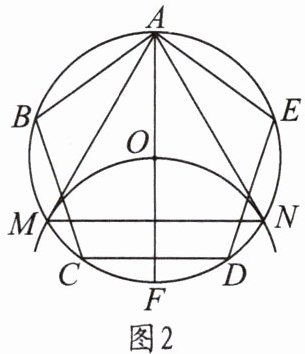
9. 如图 1，正五边形$ABCDE$内接于$\odot O$，阅读以下作图过程，并回答下列问题.作法：如图 2，
①作直径$AF$；
②以$F$为圆心、$FO$长为半径作圆弧，与$\odot O$交于点$M$，$N$；
③连结$AM$，$MN$，$NA$.
(1)求$\angle ABC$的度数.
(2)$ \bigtriangleup AMN$是正三角形吗？请说明理由.
(3)从点$A$开始，以$DN$长为半径，在$\odot O$上依次截取点，再依次连结这些分点，得到正$n$边形，求$n$的值.

答案：
9.
(1)解:
∵AB=BC=CD=DE=AE,
∴∠AOB=∠BOC=∠COD=∠DOE=∠EOA=$\frac{360}{5}$=72°,
∵AEC=3AE,
∴∠AOC(优弧所对圆心角)=3×72°=216°,
∴∠ABC=$\frac{1}{2}$∠AOC=$\frac{1}{2}$×216°=108°.
　　
(2)解:△AMN是正三角形，理由如下:
连结ON,FN,由作图知:FN=FO,
∵ON=OF,
∴ON=OF=FN,
∴△OFN是正三角形,
∴∠OFN=60°,
∴∠AMN=∠OFN=60°,同理∠ANM=60°,
∴∠MAN=60°,即∠AMN=∠ANM=∠MAN,
∴△AMN是正三角形.
(3)
∵∠AON=2∠AMN=120°,
∵AD=2AE,
∴∠AOD=2×72°=144°,
∵DN=AD−AN,
∴∠NOD=144°−120°=24°,
∴n=$\frac{360}{24}$=15.