《2025年名师面对面学科素养评价九年级数学全一册浙教版》

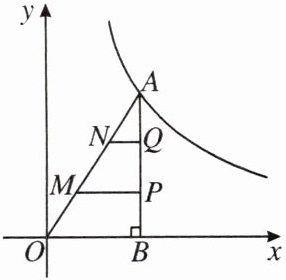
7.如图，$\triangle ABO$的顶点$A$在函数$y = \frac{k}{x}(x ＞ 0)$的图象上，$\angle ABO = 90^{\circ}$，过边$AO$的三等分点$M,N$分别作$x$轴的平行线交$AB$于点$P$，$Q$.若四边形$MNQP$的面积为 3，则$k$的值为18.

答案： 7.18

8.如图，在$\triangle ABC$中，点$D,E,F$分别在边$AB,AC,BC$上，连结$DE,EF$.已知四边形$BFED$是平行四边形，$\frac{DE}{BC} = \frac{1}{4}$.
(1)若$AB = 8$，求线段$AD$的长.
(2)若$\triangle ADE$的面积为 1，求平行四边形$BFED$的面积.

答案： 8.解：
(1)$\because$四边形 $BFED$ 是平行四边形，
$\therefore DE // BF$，$\therefore DE // BC$，
$\therefore \triangle ADE \backsim \triangle ABC$，$\therefore \frac{AD}{AB}=\frac{DE}{BC}=\frac{1}{4}$，
$\because AB=8$，$\therefore AD=2$．
(2)$\because \triangle ADE \backsim \triangle ABC$，$\therefore \frac{S_{\triangle ADE}}{S_{\triangle ABC}}=(\frac{DE}{BC})^2=\frac{1}{16}$，
$\because \triangle ADE$ 的面积为 $1$，$\therefore \triangle ABC$ 的面积是 $16$，
$\because$四边形 $BFED$ 是平行四边形，$\therefore EF // AB$，
$\therefore \triangle EFC \backsim \triangle ABC$，$\therefore \frac{S_{\triangle EFC}}{S_{\triangle ABC}}=(\frac{3}{4})^2=\frac{9}{16}$，
$\therefore S_{\triangle EFC}=9$，
$\therefore$平行四边形 $BFED$ 的面积$=16 - 9 - 1=6$．

9.在每个小正方形的边长为 1 的网格图形中，每个小正方形的顶点称为格点，顶点都是格点的三角形称为格点三角形.如图，已知$Rt \triangle ABC$是$6 × 6$网格图形中的格点三角形，则该图中所有与$Rt \triangle ABC$相似的格点三角形中，面积最大的三角形的斜边长是多少?

答案：
9.解：$\because$在 $Rt\triangle ABC$ 中，
$AC=1$，$BC=2$，
$\therefore AB=\sqrt{5}$，$AC:BC=1:2$，

$\therefore$与 $Rt\triangle ABC$ 相似的格点三角形的两直角边的比值为 $1:2$，
若该三角形最短边长为 $4$，则另一直角边长为 $8$，
但在 $6 × 6$ 网格图形中，最长线段为 $6\sqrt{2}$，
但此时画出的直角三角形为等腰直角三角形，
从而画不出端点都在格点且长为 $8$ 的线段，
故最短直角边长应小于 $4$，在图中尝试，
可画出 $DE=\sqrt{10}$，$EF=2\sqrt{10}$，$DF=5\sqrt{2}$ 的三角形，
$\because \frac{\sqrt{10}}{1}=\frac{2\sqrt{10}}{2}=\frac{5\sqrt{2}}{\sqrt{5}}=\sqrt{10}$，
$\therefore \triangle ABC \backsim \triangle DEF$，$\therefore \angle DEF=\angle C=90^{\circ}$，
$\therefore$此时 $\triangle DEF$ 的面积为：$\sqrt{10} × 2\sqrt{10} ÷ 2=10$，
$\triangle DEF$ 为面积最大的三角形，其斜边长为 $5\sqrt{2}$．