《2025年名师面对面学科素养评价九年级数学全一册浙教版》

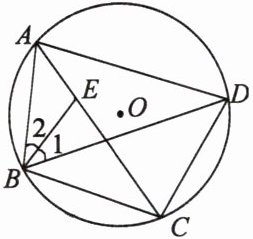
【例 3】如图,四边形 ABCD 内接于⊙O,点 E 在对角线 AC 上,EC = BC = DC.
(1)若∠CBD = 39°,求∠BAD 的度数.
(2)求证:∠1 = ∠2.

答案： 【例3】解：
(1)
∵ BC = DC,
∴ $\widehat {BC}$ = $\widehat {DC}$.
∴ ∠BAC = ∠CAD = ∠CBD.
∵ ∠CBD = 39°,
∴ ∠BAC = ∠CAD = 39°.
∴ ∠BAD = ∠BAC + ∠DAC = 78°.
(2)证明：
∵ EC = BC,
∴ ∠CBE = ∠CEB.
∵ ∠CBE = ∠1 + ∠CBD, ∠CEB = ∠2 + ∠BAC,
∴ ∠1 + ∠CBD = ∠2 + ∠BAC.
又
∵ ∠BAC = ∠CBD,
∴ ∠1 = ∠2.

【练习 5】如图,AB 是⊙O 的直径,C,D 是⊙O 上两点,且 CD = CB,CD 与 AB 交于点 E,连结 OD.若∠AOD = 80°,则∠B 的度数是 (B)
 

A.20°
B.25°
C.30°
D.35°

答案： 练习5.B

【练习 6】如图,在平面直角坐标系中,⊙P 的圆心在 x 轴上,且经过点 A(m,-3)和点 B(-1,n).点 C 是第一象限圆上的任意一点,且∠ACB = 45°,则⊙P 的圆心的坐标是(2,0)

答案： 练习6.(2,0)

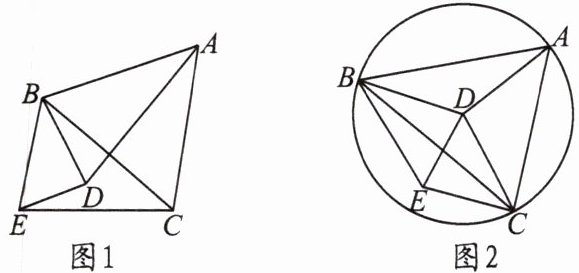
【练习 7】已知,如图 1,在△ABC 中,BA = BC,D 是平面内不与 A,B,C 重合的任意一点,∠ABC = ∠DBE,BD = BE.
(1)求证:△ABD≌△CBE.
(2)如图 2,当点 D 是△ABC 的外接圆圆心时,
①请判断四边形 BDCE 的形状,并证明你的结论.
②当∠ABC 为多少度时,点 E 在圆 D 上?请说明理由.

　

答案： 练习7.
(1)证明：
∵ ∠ABC = ∠DBE,
∴ ∠ABC + ∠CBD = ∠DBE + ∠CBD,
∴ ∠ABD = ∠CBE, 在△ABD 与△CBE 中,
∵ $\begin{cases} BA = BC, \\ ∠ABD = ∠CBE, \\ BD = BE, \end{cases}$
∴ △ABD ≌ △CBE(SAS).
(2)解：四边形BDCE是菱形.证明如下：
同
(1)可证△ABD ≌ △CBE,
∴ CE = AD,
∵ 点D是△ABC外接圆圆心,
∴ DA = DB = DC,
又
∵ BD = BE,
∴ BD = BE = CE = CD,
∴ 四边形BDCE是菱形;
②当∠ABC为60度时, ∠DBE也为60度,
△BDE为等边三角形,
∴ DE = DA,
∴ 点E在圆D上.