第55页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
7.如图,某超市计划将门前的部分楼梯改造成无障碍通道.已知楼梯共有五级均匀分布的台阶,高$AB = 0.75 m$,斜坡 AC 的坡比为$1:2$,将要铺设的通道前方有一井盖,井盖边缘离楼梯底部的最短距离$ED = 2.55 m$.为防止通道遮盖井盖,所铺设通道的坡角不得小于
参考数据表
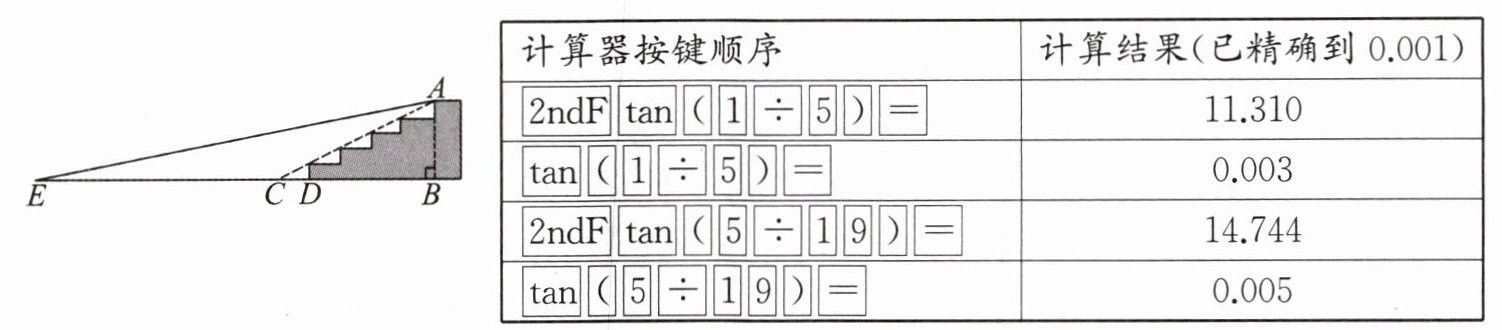
计算器按键顺序 计算结果(已精确到 0.001)
$2 ndF\tan(1÷5)=$ $11.310$
$\tan(1÷5)=$ $0.003$
$2 ndF\tan(5÷19)=$ $14.744$
$\tan(5÷19)=$ $0.005$
12
度.(结果精确到$1^{\circ}$)参考数据表

计算器按键顺序 计算结果(已精确到 0.001)
$2 ndF\tan(1÷5)=$ $11.310$
$\tan(1÷5)=$ $0.003$
$2 ndF\tan(5÷19)=$ $14.744$
$\tan(5÷19)=$ $0.005$
答案:
7.12
8.知识小提示:要想使人安全地攀上斜靠在墙面上的梯子的顶端,梯子与地面所成的角$\alpha$一般要满足$53^{\circ}\leq\alpha\leq72^{\circ}$.现有一架长$4 m$的梯子$AB$斜靠在一竖直的墙$AO$上.
(1)当人安全使用这架梯子时,求梯子顶端$A$与地面距离的最大值.
(2)当梯子底端$B$距离墙面$1.64 m$时,计算$\angle ABO$等于多少度?此时人是否能安全使用这架梯子?
(参考数据:$\sin53^{\circ}\approx0.80$,$\cos53^{\circ}\approx0.60$,$\tan53^{\circ}\approx1.33$,$\sin72^{\circ}\approx0.95$,$\cos72^{\circ}\approx0.31$,$\tan72^{\circ}\approx3.08$,$\sin66^{\circ}\approx0.91$,$\cos66^{\circ}\approx0.41$,$\tan66^{\circ}\approx2.25$)
(1)当人安全使用这架梯子时,求梯子顶端$A$与地面距离的最大值.
(2)当梯子底端$B$距离墙面$1.64 m$时,计算$\angle ABO$等于多少度?此时人是否能安全使用这架梯子?
(参考数据:$\sin53^{\circ}\approx0.80$,$\cos53^{\circ}\approx0.60$,$\tan53^{\circ}\approx1.33$,$\sin72^{\circ}\approx0.95$,$\cos72^{\circ}\approx0.31$,$\tan72^{\circ}\approx3.08$,$\sin66^{\circ}\approx0.91$,$\cos66^{\circ}\approx0.41$,$\tan66^{\circ}\approx2.25$)

答案:
8.解:
(1)53° ≤ α ≤ 72°,当α=72°时,AO取最大值,
∴AO=AB·sin∠ABO=4×sin72°=4×0.95=3.8(米),
∴梯子顶端A与地面的距离的最大值为3.8米.
(2)在Rt△AOB中$,cos∠ABO= \frac{BO}{AB}=1.64÷4=0.41,$
∵cos66°≈0.41,
∴∠ABO=66°,
∵53° ≤ α ≤ 72°,
∴人能安全使用这架梯子.
(1)53° ≤ α ≤ 72°,当α=72°时,AO取最大值,
∴AO=AB·sin∠ABO=4×sin72°=4×0.95=3.8(米),
∴梯子顶端A与地面的距离的最大值为3.8米.
(2)在Rt△AOB中$,cos∠ABO= \frac{BO}{AB}=1.64÷4=0.41,$
∵cos66°≈0.41,
∴∠ABO=66°,
∵53° ≤ α ≤ 72°,
∴人能安全使用这架梯子.
9.数学教师布置了这样一个问题:如果$\alpha,\beta$都为锐角,且$\tan\alpha=\frac{1}{2},\tan\beta=\frac{1}{3}$,求$\alpha+\beta$的度数.
甲、乙两位同学想利用正方形网格构图来解决问题,他们分别设计了图 1 和图 2.
(1)请你分别利用图 1、图 2 求出$\alpha+\beta$的度数,并说明理由.
(2)请参考以上思考问题的方法,选择一种方法解决下面问题:如果$\alpha,\beta$都为锐角,当$\tan\alpha = 5$,$\tan\beta=\frac{2}{3}$时,在图 3 的正方形网格中,利用已作出的锐角$\alpha$,画出$\angle MON$,使得$\angle MON=\alpha - \beta$,求出$\alpha - \beta$的度数,并说明理由.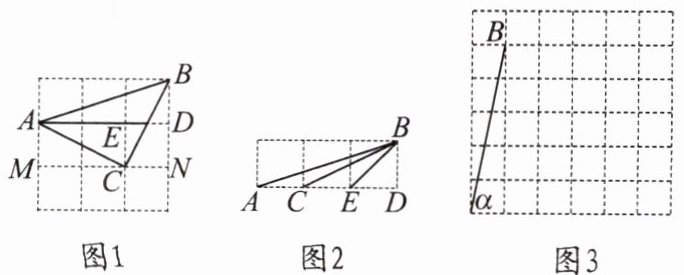
甲、乙两位同学想利用正方形网格构图来解决问题,他们分别设计了图 1 和图 2.
(1)请你分别利用图 1、图 2 求出$\alpha+\beta$的度数,并说明理由.
(2)请参考以上思考问题的方法,选择一种方法解决下面问题:如果$\alpha,\beta$都为锐角,当$\tan\alpha = 5$,$\tan\beta=\frac{2}{3}$时,在图 3 的正方形网格中,利用已作出的锐角$\alpha$,画出$\angle MON$,使得$\angle MON=\alpha - \beta$,求出$\alpha - \beta$的度数,并说明理由.

答案:
9.解:
(1)①如图1中,
易证△AMC≌△CNB.
∴AC=BC,∠ACM=∠CBN.
∵∠BCN+∠CBN=90°,
∴∠ACM+∠BCN=90°.
∴∠ACB=90°,
∴∠CAB=∠CBA=45°.
∴α+β=45°.
②如图2中,易证△CEB∽△BEA.
∴∠CAB=∠CBE=β.
∴∠BED=∠ECB+∠CBE=α+β.
∵DE=DB,∠D=90°,∠BED=45°,
∴α+β=45°.
(2)如答图中,∠MOE=α,∠NOH=β,
∠MON=α - β.
 易证△MFN≌△NHO.
易证△MFN≌△NHO.
∴MN=NO,
∠MNF=∠NOH.
∵∠NOH+∠ONH=90°,
∴∠ONH+∠MNF=90°.
∴∠MNO=90°.
∴∠NOM=∠NMO=45°.
∴α - β=45°.
9.解:
(1)①如图1中,
易证△AMC≌△CNB.
∴AC=BC,∠ACM=∠CBN.
∵∠BCN+∠CBN=90°,
∴∠ACM+∠BCN=90°.
∴∠ACB=90°,
∴∠CAB=∠CBA=45°.
∴α+β=45°.
②如图2中,易证△CEB∽△BEA.
∴∠CAB=∠CBE=β.
∴∠BED=∠ECB+∠CBE=α+β.
∵DE=DB,∠D=90°,∠BED=45°,
∴α+β=45°.
(2)如答图中,∠MOE=α,∠NOH=β,
∠MON=α - β.
 易证△MFN≌△NHO.
易证△MFN≌△NHO.∴MN=NO,
∠MNF=∠NOH.
∵∠NOH+∠ONH=90°,
∴∠ONH+∠MNF=90°.
∴∠MNO=90°.
∴∠NOM=∠NMO=45°.
∴α - β=45°.
查看更多完整答案,请扫码查看


