第58页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
1.一艘海轮位于灯塔 $P$ 的北偏东$55^{\circ}$方向,距离灯塔 2 海里的点 $A$ 处.如果海轮沿正南方向航行到灯塔的正东方向,那么海轮航行的距离 $AB$ 是 (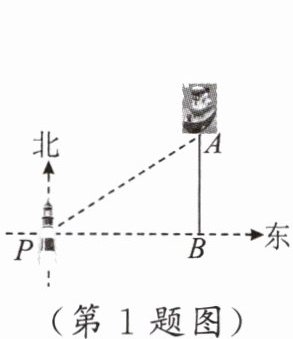
A.2 海里
B.$2\sin 55^{\circ}$海里
C.$2\cos 55^{\circ}$海里
D.$2\tan 55^{\circ}$海里
C
)
A.2 海里
B.$2\sin 55^{\circ}$海里
C.$2\cos 55^{\circ}$海里
D.$2\tan 55^{\circ}$海里
答案:
1.C
2.如图,在离铁塔 150 米的 $A$ 处,用测倾仪测得塔顶的仰角为 $\alpha$,测倾仪高 $AD$ 为 1.5 米,则铁塔的高 $BC$ 为 (
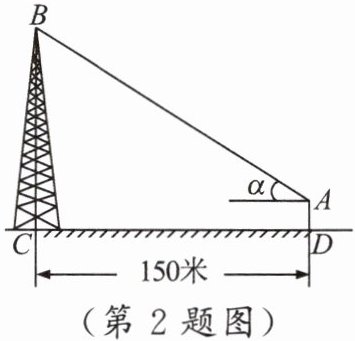
A.$(1.5 + 150\tan\alpha)$米
B.$(1.5+\frac{150}{\tan\alpha})$米
C.$(1.5 + 150\sin\alpha)$米
D.$(1.5+\frac{150}{\sin\alpha})$米
A
)
A.$(1.5 + 150\tan\alpha)$米
B.$(1.5+\frac{150}{\tan\alpha})$米
C.$(1.5 + 150\sin\alpha)$米
D.$(1.5+\frac{150}{\sin\alpha})$米
答案:
2.A
3.如图,一条船从海岛 $A$ 出发,以 15 海里/时的速度向正北航行,2 小时后到达海岛 $B$ 处.灯塔 $C$ 在海岛 $A$ 的北偏西 $42^{\circ}$方向上,在海岛 $B$ 的北偏西 $84^{\circ}$方向上,则海岛 $B$ 到灯塔 $C$ 的距离是 (
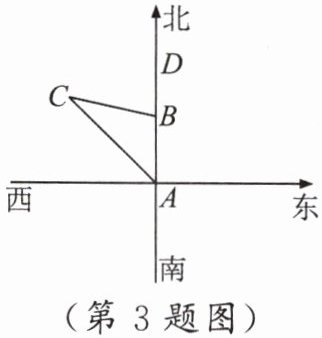
A.15 海里
B.20 海里
C.30 海里
D.60 海里
C
)
A.15 海里
B.20 海里
C.30 海里
D.60 海里
答案:
3.C
4.如图,校园内有一株枯死的大树 $AB$,距树 12 米处有一栋教学楼 $CD$,为了安全,学校决定砍伐该树.站在楼顶 $D$,测得点 $B$ 的仰角为 $45^{\circ}$,点 $A$ 的俯角为 $30^{\circ}$.小青计算后得到如下结论:①$AB\approx18.8$;②$CD\approx8.4$米;③若直接从点 $A$ 处砍伐,树干倒向教学楼 $CD$ 方向会对教学楼有影响;④若第一次在距点 $A$ 的 8 米处的树干上砍伐,不会对教学楼 $CD$ 造成危害.其中正确的是
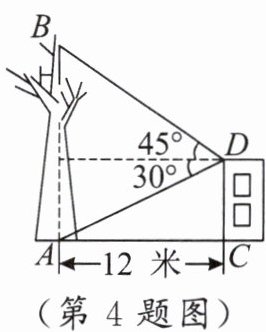
①③④
.(填写序号,参考数据:$\sqrt{3}\approx1.7$,$\sqrt{2}\approx1.4$)
答案:
4.①③④
5.如图,测得两楼之间的水平距离为 32 m,从楼顶点 $A$ 观测点 $D$ 的俯角为 $45^{\circ}$,观测点 $C$ 的俯角为 $58^{\circ}$.分别求这两幢楼的高度.(结果精确到 1 m,参考数据:$\sin 58^{\circ}\approx0.85$,$\cos 58^{\circ}\approx0.53$,$\tan 58^{\circ}\approx1.60$)
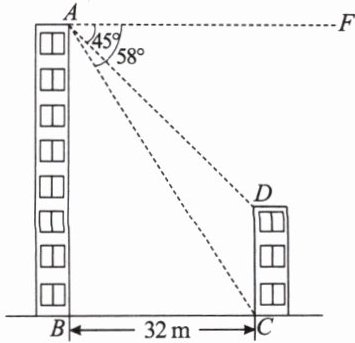

答案:
5.解:如图,过D作DE⊥AB于E,
∴∠AED=90°,

∴∠AED=∠EBC=∠DCB=90°,
∴四边形BCDE是矩形,
∴DE=BC=32m,BE=DC,
在Rt△ABC中,∠ACB=58°,
∴AB=BCtan∠ACB=32×tan58°≈32×1.60≈51(m),
∴BE=CD=AB−AE≈51−32=19(m).
答:建筑物AB的高约为51m,CD的高约为19m.
5.解:如图,过D作DE⊥AB于E,
∴∠AED=90°,

∴∠AED=∠EBC=∠DCB=90°,
∴四边形BCDE是矩形,
∴DE=BC=32m,BE=DC,
在Rt△ABC中,∠ACB=58°,
∴AB=BCtan∠ACB=32×tan58°≈32×1.60≈51(m),
∴BE=CD=AB−AE≈51−32=19(m).
答:建筑物AB的高约为51m,CD的高约为19m.
查看更多完整答案,请扫码查看


