《2025年名师面对面学科素养评价九年级数学全一册浙教版》

6.某校数学社团开展“探索生活中的数学”研学活动，准备测量一栋大楼 $BC$ 的高度.如图所示，其中观景平台斜坡 $DE$ 的长是 20 米，坡角为 $37^{\circ}$，斜坡 $DE$ 底部 $D$ 与大楼底端 $C$ 的距离 $CD$ 为 74 米，与地面 $CD$ 垂直的路灯 $AE$ 的高度是 3 米，从楼顶 $B$ 测得路灯 $AE$ 顶端 $A$ 处的俯角是 $42.6^{\circ}$.试求大楼 $BC$ 的高度.
（参考数据：$\sin 37^{\circ}\approx\frac{3}{5}$，$\cos 37^{\circ}\approx\frac{4}{5}$，$\tan 37^{\circ}\approx\frac{3}{4}$，$\sin 42.6^{\circ}\approx\frac{17}{25}$，$\cos 42.6^{\circ}\approx\frac{33}{45}$，$\tan 42.6^{\circ}\approx\frac{9}{10}$）

答案：
6.解:延长AE交CD的延长线于M，
过A作AN⊥BC于N,如图所示，

则四边形AMCN是矩形，
∴NC=AM,AN=MC,
在Rt△EMD中,∠EDM=37°,
EM=ED×sin37°≈20×$\frac{3}{5}$=12(米)，
DM=ED×cos37°≈20×$\frac{4}{5}$=16(米)，
∴AN=MC=CD+DM=74+16=90(米),
在Rt△ANB中,∠BAN=42.6°,
BN=AN×tan42.6°≈90×$\frac{9}{10}$=81(米)，
∴BC=BN+AE+EM=81+3+12=96(米),
答:大楼BC的高度约为96米.

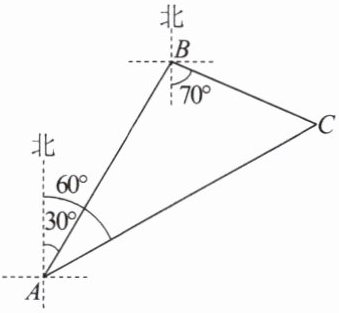
7.如图，一艘货轮在海面上航行，准备要停靠到码头 $C$，货轮航行到 $A$ 处时，测得码头 $C$ 在北偏东 $60^{\circ}$方向上.为了躲避 $A$，$C$ 之间的暗礁，这艘货轮调整航向，沿着北偏东 $30^{\circ}$方向继续航行，当它航行到 $B$ 处后，又沿着南偏东 $70^{\circ}$方向航行 20 海里到达码头 $C$.求货轮从 $A$ 到 $B$ 航行的距离.(结果精确到 0.1 海里，参考数据：$\sin 50^{\circ}\approx0.766$，$\cos 50^{\circ}\approx0.643$，$\tan 50^{\circ}\approx1.192$)

答案：
7.解:过B作BD⊥AC于D,由题意可知:
∠ABE=30°,∠BAC=30°,
则∠C=180°−30°−30°−70°=50°,

在Rt△BCD中,∠C=50°,BC=20(海里),
∴BD=BCsin50°≈20×0.766=15.32(海里),
在Rt△ABD中,∠BAD=30°,BD=15.32(海里),
∴AB=2BD=30.64≈30.6(海里).
答:货轮从A到B航行的距离约为30.6海里.