《2025年名师面对面学科素养评价九年级数学全一册浙教版》

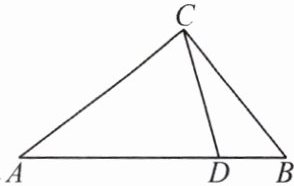
7. 从三角形(非等腰三角形)的一个顶点引出一条射线与对边相交，该顶点与该交点间的线段把这个三角形分割成两个小三角形.如果其中一个小三角形是等腰三角形，另一个与原三角形相似，那么我们把这条线段叫作这个三角形的完美分割线.如图，在$\triangle ABC$中，$DB = 1$，$BC = 2$，$CD$是$\triangle ABC$的完美分割线，且$\triangle ACD$是以$CD$为底边的等腰三角形，则$CD$的长为$\frac {3}{2}$.

答案： 7.$\frac {3}{2}$

8. 如图，在矩形$ABCD$中，点$E$，$F$分别在边$AD$，$DC$上，$\triangle ABE \sim \triangle DEF$，$AB = 6$，$AE = 9$，$DE = 2$.
(1)求$EF$的长.

(2)求证：$\angle BEF = 90^{\circ}$.

答案： 解：
(1)在Rt△ABE中，
$BE=\sqrt {AB^{2}+AE^{2}}=3\sqrt {13}$，
∵△ABE∽△DEF，
$\therefore \frac {EF}{BE}=\frac {DE}{AB}$,即$\frac {EF}{3\sqrt {13}}=\frac {2}{6}$,$\therefore EF=\sqrt {13}$．
(2)证明：
∵△ABE∽△DEF，$\therefore \angle AEB=\angle DFE$．
又
∵$\angle DEF+\angle DFE=90^{\circ}$,$\angle DEF+\angle AEB=90^{\circ}$，
$\therefore \angle BEF=90^{\circ}$．

9. 一个钢筋三脚架长分别是$20 cm$，$50 cm$，$60 cm$.现要再做一个与其相似的钢筋三脚架，而只有长为$30 cm$和$50 cm$的两根钢筋，要求以其中一根为一边，从另一根上截下两段（允许有余料），作为其余两边，则不同的截法有多少种？请说明理由.

答案： 解：设截下的两边长为$x$ cm,$y$ cm,且$x＜y$.假如将30cm的
钢筋截开，则$x+y=30＜50$，不能构成三角形，所以必须将
50cm的钢筋截开．
①当30cm与60cm是对应边时,$\frac {20}{x}=\frac {50}{y}=\frac {60}{30}$，
$x=10$,$y=25$，而$10+25＜50$，故这种情况成立；
②当30cm与50cm是对应边时,$\frac {20}{x}=\frac {50}{30}=\frac {60}{y}$，
$x=12$,$y=36$，而$12+36＜50$，故这种情况也成立；
③当30cm与20cm是对应边时,$\frac {20}{30}=\frac {50}{x}=\frac {60}{y}$，
$x=75$,$y=90$，而$75+90＞50$，故这种情况不成立．
综上所述，有两种不同的截法．