第40页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
1. 如图,若$\triangle ABC \sim \triangle DEF$,则$\angle C$的度数是 (
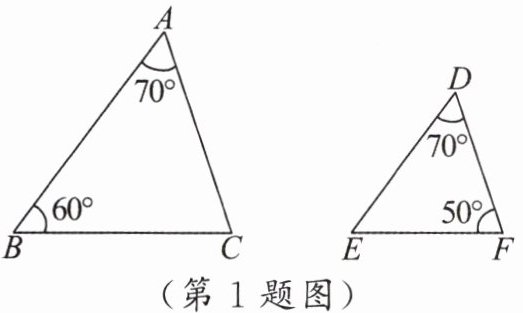
A.$70^{\circ}$
B.$60^{\circ}$
C.$50^{\circ}$
D.$40^{\circ}$
C
)
A.$70^{\circ}$
B.$60^{\circ}$
C.$50^{\circ}$
D.$40^{\circ}$
答案:
1.C
2. 如图,$\triangle ABC \sim \triangle A'B'C'$,下列说法正确的是 (
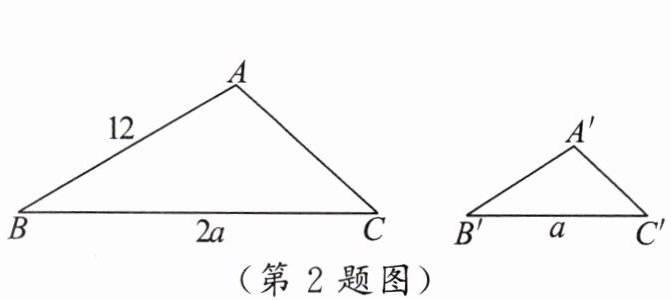
A.$\angle B = \angle C'$
B.$A'C' = 6$
C.$AC = 4A'C'$
D.$A'B' = 6$
D
)
A.$\angle B = \angle C'$
B.$A'C' = 6$
C.$AC = 4A'C'$
D.$A'B' = 6$
答案:
2.D
3. 要制作两个形状相同的三角形框架,其中一个三角形的三边长分别为$5 cm$,$6 cm$和$9 cm$,另一个三角形的最短边长为$2.5 cm$,则它的最长边为 (
A.$3 cm$
B.$4 cm$
C.$4.5 cm$
D.$5 cm$
C
)A.$3 cm$
B.$4 cm$
C.$4.5 cm$
D.$5 cm$
答案:
3.C
4. 如图,在$\triangle ABC$中,$BC = 3$,$AC = 4$.若$\triangle ABC \sim \triangle BDC$,则$CD$等于 (
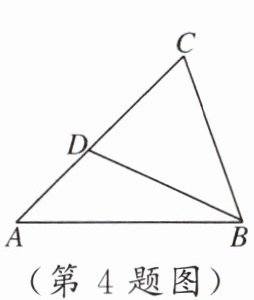
A.$2$
B.$\frac{3}{2}$
C.$\frac{4}{3}$
D.$\frac{9}{4}$
D
)
A.$2$
B.$\frac{3}{2}$
C.$\frac{4}{3}$
D.$\frac{9}{4}$
答案:
4.D
5. 如图,$\triangle ABC \sim \triangle ADE$,$BC$的延长线经过点$E$,交$AD$于点$F$,$\angle ACB = \angle AED = 105^{\circ}$,$\angle CAD = 10^{\circ}$,$\angle B = 50^{\circ}$,则$\angle EAB =$

60
$^{\circ}$.
答案:
5.60
6. 如图,已知$AD = 3 cm$,$AC = 6 cm$,$BC = 9 cm$,$\angle B = 36^{\circ}$,$\angle D = 117^{\circ}$,$\triangle ABC \sim \triangle DAC$.
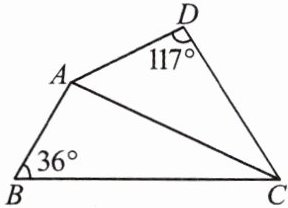
(1)求$AB$的长.
(2)求$\angle BAD$的大小.

(1)求$AB$的长.
(2)求$\angle BAD$的大小.
答案:
解:
(1)
∵△ABC∽△DAC,
$\therefore \frac {AB}{AD}=\frac {BC}{AC}$,$\therefore \frac {AB}{3}=\frac {9}{6}$,
$\therefore AB=4.5(cm)$.
(2)
∵△ABC∽△DAC,
$\therefore \angle BAC=\angle D=117^{\circ}$,
$\angle CAD=\angle B=36^{\circ}$,
$\therefore \angle BAD=\angle BAC+\angle CAD=117^{\circ}+36^{\circ}=153^{\circ}$.
(1)
∵△ABC∽△DAC,
$\therefore \frac {AB}{AD}=\frac {BC}{AC}$,$\therefore \frac {AB}{3}=\frac {9}{6}$,
$\therefore AB=4.5(cm)$.
(2)
∵△ABC∽△DAC,
$\therefore \angle BAC=\angle D=117^{\circ}$,
$\angle CAD=\angle B=36^{\circ}$,
$\therefore \angle BAD=\angle BAC+\angle CAD=117^{\circ}+36^{\circ}=153^{\circ}$.
查看更多完整答案,请扫码查看


