第23页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
7.小明把一副三角尺按如图所示叠放在一起,固定三角尺$ABC$,将另一块三角尺$DEF$绕公共顶点$B$顺时针旋转(旋转的度数不超过$180^{\circ}$).若两块三角尺有一边平行,则三角尺$DEF$旋转的度数可能是
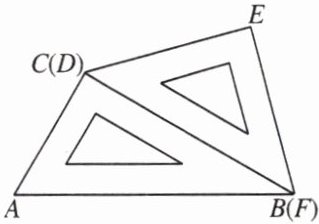
15°或45°或90°或135°
.
答案:
7.15°或45°或90°或135°
8.如图所示,正方形$ABCD$的边$BC$上有一点$E$,$\angle DAE$的平分线交$CD$于点$F$.
求证:$AE = DF + BE$.
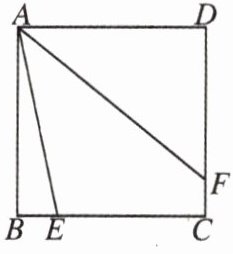
求证:$AE = DF + BE$.

答案:
8.证明:如图所示,将△ADF绕点A 顺时针旋转90°得到△ABF'.则∠3 =∠1,∠AFD=∠F',∠ABF'=∠D,BF'=DF.
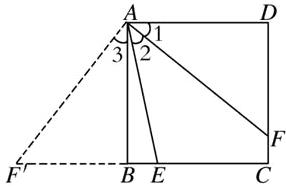
∵四边形ABCD为正方形,
∴AB//CD,∠ABC=∠D=90°,
∴∠AFD=∠FAB,∠ABF'=∠D=90°,
∴∠ABF'+∠ABC=180°,
∴F',B,C三点共线.
∵∠FAB=∠2+∠BAE,
∴∠AFD=∠2+∠BAE.
又
∵∠DAE的平分线交CD于点F,
∴∠1=∠2,
∴∠3=∠2,
∴∠AFD=∠3+∠BAE,
∴∠F'=∠3+∠BAE.
∵∠F'AE=∠3+∠BAE,
∴∠F'AE=∠F',
∴AE=EF'=BF'+BE=DF+BE.
8.证明:如图所示,将△ADF绕点A 顺时针旋转90°得到△ABF'.则∠3 =∠1,∠AFD=∠F',∠ABF'=∠D,BF'=DF.

∵四边形ABCD为正方形,
∴AB//CD,∠ABC=∠D=90°,
∴∠AFD=∠FAB,∠ABF'=∠D=90°,
∴∠ABF'+∠ABC=180°,
∴F',B,C三点共线.
∵∠FAB=∠2+∠BAE,
∴∠AFD=∠2+∠BAE.
又
∵∠DAE的平分线交CD于点F,
∴∠1=∠2,
∴∠3=∠2,
∴∠AFD=∠3+∠BAE,
∴∠F'=∠3+∠BAE.
∵∠F'AE=∠3+∠BAE,
∴∠F'AE=∠F',
∴AE=EF'=BF'+BE=DF+BE.
9.将矩形$ABCD$绕点$A$顺时针旋转$\alpha(0^{\circ}<\alpha<360^{\circ})$,得到矩形$AEFG$.
(1)如图,当点$E$在$BD$上时.求证:$FD = CD$.
(2)当$\alpha$为何值时,$GC = GB$?画出图形,并说明理由.
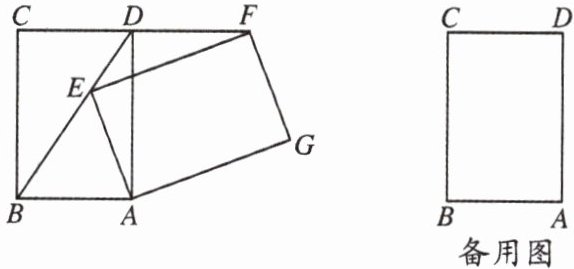
(1)如图,当点$E$在$BD$上时.求证:$FD = CD$.
(2)当$\alpha$为何值时,$GC = GB$?画出图形,并说明理由.

答案:
9.解:
(1)由旋转可得,AE=AB,∠AEF=∠ABC=∠DAB=90°,EF=BC=AD,
∴∠AEB=∠ABE,
又
∵∠ABE+∠EDA=90°=∠AEB+∠DEF,
∴∠EDA=∠DEF,又
∵DE=ED,
∴△AED≌△FDE(SAS),
∴DF=AE,
又
∵AE=AB=CD,
∴CD=DF.
(2)如图,当GB=GC时,点G在BC的垂直平分线上,
分两种情况讨论:
①当点G在AD右侧时,取BC的中点H,连结GH交AD 于M,
∵GC=GB,
∴GH⊥BC,
∴四边形ABHM是矩形,
∴AM=BH=$\frac{1}{2}$AD=$\frac{1}{2}$AG,
∴GM垂直平分AD,
∴GD=GA=DA,
∴△ADG是等边三角形,
∴∠DAG=60°,
∴旋转角α=60°.
②当点G在AD左侧时,同理可得△ADG是等边三角形,
∴∠DAG=60°,
∴旋转角α=360°−60°=300°.


9.解:
(1)由旋转可得,AE=AB,∠AEF=∠ABC=∠DAB=90°,EF=BC=AD,
∴∠AEB=∠ABE,
又
∵∠ABE+∠EDA=90°=∠AEB+∠DEF,
∴∠EDA=∠DEF,又
∵DE=ED,
∴△AED≌△FDE(SAS),
∴DF=AE,
又
∵AE=AB=CD,
∴CD=DF.
(2)如图,当GB=GC时,点G在BC的垂直平分线上,
分两种情况讨论:
①当点G在AD右侧时,取BC的中点H,连结GH交AD 于M,
∵GC=GB,
∴GH⊥BC,
∴四边形ABHM是矩形,
∴AM=BH=$\frac{1}{2}$AD=$\frac{1}{2}$AG,
∴GM垂直平分AD,
∴GD=GA=DA,
∴△ADG是等边三角形,
∴∠DAG=60°,
∴旋转角α=60°.
②当点G在AD左侧时,同理可得△ADG是等边三角形,
∴∠DAG=60°,
∴旋转角α=360°−60°=300°.


查看更多完整答案,请扫码查看


