第50页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
【例 1】(1)已知线段$m = 8$,$n = 2$,求线段$m$,$n$的比例中项.
(2)已知$\frac{x}{3} = \frac{y}{5}$,$x + y = 24$,求$x$,$y$的值.
(2)已知$\frac{x}{3} = \frac{y}{5}$,$x + y = 24$,求$x$,$y$的值.
答案:
解:
(1)
∵线段$m = 8,n = 2$,
∴线段$m,n$的比例中项$ = \sqrt{8 × 2} = 4$.
(2)设$\frac{x}{3} = \frac{y}{5} = k$,可得$x = 3k,y = 5k$,
把$x = 3k,y = 5k$代入$x + y = 24$,可得$3k + 5k = 24$,解得$k = 3$,所以$x = 3 × 3 = 9,y = 3 × 5 = 15$.
(1)
∵线段$m = 8,n = 2$,
∴线段$m,n$的比例中项$ = \sqrt{8 × 2} = 4$.
(2)设$\frac{x}{3} = \frac{y}{5} = k$,可得$x = 3k,y = 5k$,
把$x = 3k,y = 5k$代入$x + y = 24$,可得$3k + 5k = 24$,解得$k = 3$,所以$x = 3 × 3 = 9,y = 3 × 5 = 15$.
练习1如果舞台$AB$的长为$10$米,一名主持人现在站在$A$处,那么她至少走多少米才到达舞台的黄金分割点处
(
A.$5\sqrt{5} - 5$
B.$15 - 5\sqrt{5}$
C.$5\sqrt{5} + 5$
D.$15 - 5\sqrt{5}$或$5\sqrt{5} - 5$
(
B
)A.$5\sqrt{5} - 5$
B.$15 - 5\sqrt{5}$
C.$5\sqrt{5} + 5$
D.$15 - 5\sqrt{5}$或$5\sqrt{5} - 5$
答案:
练习1.B
【例 2】已知:如图,在菱形$ABCD$中,点$E$,$F$分别在边$BC$,$CD$上,$BE = FD$,$AF$的延长线交$BC$的延长线于点$H$,$AE$的延长线交$DC$的延长线于点$G$.

(1)求证:$\bigtriangleup AFD \backsim \bigtriangleup GAD$.
(2)若$DF^{2} = CF · CD$,求证:$BE = CH$.

(1)求证:$\bigtriangleup AFD \backsim \bigtriangleup GAD$.
(2)若$DF^{2} = CF · CD$,求证:$BE = CH$.
答案:
(1)证明:易证$\triangle ABE \cong \triangle ADF(SAS)$,
∴$\angle BAE = \angle DAF$.
∵$AB // CD$,
∴$\angle G = \angle BAE = \angle DAF$,
又
∵$\angle D = \angle D$,
∴$\triangle AFD \backsim \triangle GAD$.
(2)证明:
∵$DF^{2} = CF · CD$,
∴$\frac{CF}{DF} = \frac{DF}{CD}$,
∵$AD // BH$,
∴$\frac{CF}{DF} = \frac{CH}{AD}$,
∴$\frac{CH}{AD} = \frac{DF}{CD}$,
∵$AD = CD$,
∴$CH = DF$,
∵$BE = DF$,
∴$BE = CH$.
(1)证明:易证$\triangle ABE \cong \triangle ADF(SAS)$,
∴$\angle BAE = \angle DAF$.
∵$AB // CD$,
∴$\angle G = \angle BAE = \angle DAF$,
又
∵$\angle D = \angle D$,
∴$\triangle AFD \backsim \triangle GAD$.
(2)证明:
∵$DF^{2} = CF · CD$,
∴$\frac{CF}{DF} = \frac{DF}{CD}$,
∵$AD // BH$,
∴$\frac{CF}{DF} = \frac{CH}{AD}$,
∴$\frac{CH}{AD} = \frac{DF}{CD}$,
∵$AD = CD$,
∴$CH = DF$,
∵$BE = DF$,
∴$BE = CH$.
练习2如图,在$\bigtriangleup ABC$的外接圆$O$中,$D$是$\overset{\frown}{BC}$的中点,$AD$交$BC$于点$E$,连结$BD$.
(1)列出图中所有相似三角形.
(2)连结$DC$,若在$\overset{\frown}{BAC}$上任取一点$K$(点$A$,$B$,$C$除外),连结$CK$,$DK$,$DK$交$BC$于点$F$,$DC^{2} = DF · DK$是否成立?若成立,给出证明;若不成立,举例说明.
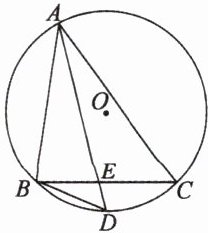
(1)列出图中所有相似三角形.
(2)连结$DC$,若在$\overset{\frown}{BAC}$上任取一点$K$(点$A$,$B$,$C$除外),连结$CK$,$DK$,$DK$交$BC$于点$F$,$DC^{2} = DF · DK$是否成立?若成立,给出证明;若不成立,举例说明.

答案:
解:
(1)$\triangle BDE \backsim \triangle ACE$,
$\triangle DBE \backsim \triangle DAB$,
$\triangle ABD \backsim \triangle AEC$.

(2)$DC^{2} = DF · DK$成立.
证明:
∵$D$是$\overset{\frown}{BC}$的中点,
∴$\overset{\frown}{BD} = \overset{\frown}{DC}$,
∴$\angle DBC = \angle DCB$(等弧的圆周角相等),
又
∵$\angle DBC = \angle DKC$,
∴$\angle DCB = \angle DKC$,
又
∵$\angle KDC = \angle CDF$,
∴$\triangle KDC \backsim \triangle CDF$,
∴$\frac{KD}{DC} = \frac{DC}{DF}$,
∴$DC^{2} = DF · DK$.
解:
(1)$\triangle BDE \backsim \triangle ACE$,
$\triangle DBE \backsim \triangle DAB$,
$\triangle ABD \backsim \triangle AEC$.

(2)$DC^{2} = DF · DK$成立.
证明:
∵$D$是$\overset{\frown}{BC}$的中点,
∴$\overset{\frown}{BD} = \overset{\frown}{DC}$,
∴$\angle DBC = \angle DCB$(等弧的圆周角相等),
又
∵$\angle DBC = \angle DKC$,
∴$\angle DCB = \angle DKC$,
又
∵$\angle KDC = \angle CDF$,
∴$\triangle KDC \backsim \triangle CDF$,
∴$\frac{KD}{DC} = \frac{DC}{DF}$,
∴$DC^{2} = DF · DK$.
查看更多完整答案,请扫码查看


