《2025年名师面对面学科素养评价九年级数学全一册浙教版》

1.在 $ Rt \triangle ABC$ 中，$\angle C = 90°$，$\sin A = \frac{3}{5}$，$BC = 6$，则 $AB$ 的长为 (D)

A.$4$
B.$6$
C.$8$
D.$10$

答案： 1.D

2.为了解决楼房之间的采光问题，某市有关部门规定：两幢楼房之间的最小距离要使中午 $12$ 时不能遮光.如图，旧楼的一楼窗台高 $1$ 米，现计划在旧楼右侧 $50$ 米处再建一幢新楼.若该市冬天中午 $12$ 时太阳照射的光线与水平线的夹角最小为 $\alpha$ 度，则新楼最高可建 (C)


A.$50 \tan \alpha$ 米
B.$\frac{50}{\tan \alpha}$ 米
C.$(50 \tan \alpha + 1)$ 米
D.$(\frac{50}{\tan \alpha} + 1)$ 米

答案： 2.C

3.在 $ Rt \triangle ABC$ 中，$\angle C = 90°$，$AB = 2\sqrt{7}$，$AC = \sqrt{21}$，则 $\angle A =$ (D)

A.$75°$
B.$60°$
C.$45°$
D.$30°$

答案： 3.D

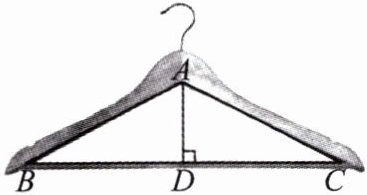
4.如图所示的衣架可以近似看成一个等腰三角形 $ABC$，其中 $AB = AC$，$\angle ABC = 27°$，$BC = 44 cm$，则高 $AD$ 约为(参考数据：$\sin 27° \approx 0.45$，$\cos 27° \approx 0.89$，$\tan 27° \approx 0.51$) (B)


A.$9.90 cm$
B.$11.22 cm$
C.$19.58 cm$
D.$22.44 cm$

答案： 4.B

5.在 $ Rt \triangle ABC$ 中，$\angle C = 90°$，$a$，$b$，$c$ 分别为 $\angle A$，$\angle B$，$\angle C$ 的对边，$c = 10$，$\angle A = 45°$，则 $a =$5$\sqrt{2}$，$b =$5$\sqrt{2}$，$\angle B =$45$°$.

答案： 5.5$\sqrt{2}$　5$\sqrt{2}$　45

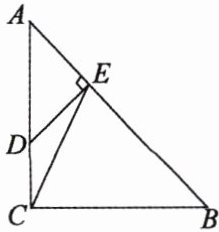
6.如图，在 $ Rt \triangle ABC$ 中，$\angle ACB = 90°$，$AC = BC = 3$，点 $D$ 在边 $AC$ 上，且 $AD = 2CD$，$DE \perp AB$，垂足为点 $E$，连结 $CE$，求：
(1)线段 $BE$ 的长.
(2)$\angle ECB$ 的正切值.

答案：
6.解:
(1)在Rt△ABC中,∠ACB = 90°,AC = BC = 3，
∴∠A = ∠B = 45°,AB = $\sqrt{AC^{2} + BC^{2}}$ = 3$\sqrt{2}$，
∵DE ⊥ AB,
∴∠AED = 90°,∠ADE = ∠A = 45°，
∴AE = AD · cos45° = $\sqrt{2}$,
∴BE = AB - AE = 2$\sqrt{2}$。
(2)过点E作EH ⊥ BC，垂足为点H，
∵在Rt△BEH中,∠EHB = 90°,∠B = 45°，
　　　　　　　　　　　　　　　　　　　　　
∴EH = BH = BE · cos45° = 2,
∵BC = 3，
∴CH = 1，
　在Rt△CHE中,tan∠ECB = $\frac{EH}{CH}$ = 2。