《2025年拔尖特训六年级数学上册苏教版江苏专版》

(1)$A:B= 3:7$,若$A+B= 40$,则$A=$12；若$B-A= 40$,则$B=$70；若$A= 40$,则$B=$$\frac{280}{3}$；若$A$、$B$的平均数是40,则$A=$24。

答案： 12 70 $\frac{280}{3}$ 24

(2) 迪迪和欢欢存的钱数的比是$3:5$。
① 若迪迪再存入400元就和欢欢存的钱一样多,则欢欢存了(1000)元。
② 若欢欢从存的钱里转100元给迪迪,则两人存的钱数相等,欢欢原来存了(500)元。
③ 若欢欢花去90元,迪迪花去50元,则他们剩下的钱数相等,欢欢原来存了(100)元。

答案： ①1000 ②500 ③100 解析:若欢欢花去90元，迪迪花去50元，则他们剩下的钱数相等，说明原来欢欢比迪迪多存90 - 50 = 40(元)，欢欢原来存了$40÷(5 - 3)×5 = 100$(元)。

(3)(五育并举)同学们参加植树活动,分为两组。第一组有59人,第二组有37人。从第二组调(13)人到第一组,就能使第一组与第二组人数的比是$3:1$。

答案： 13 解析:在调动过程中，总人数没有发生变化。

2. 一种甜品由巧克力、花生和奶粉按下图所示的比加工而成。

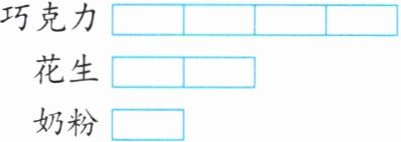
(1) 加工210千克这种甜品,巧克力、花生和奶粉分别需要多少千克？
(2) 如果三种原料分别购进40千克,要想把花生用完,那么还需购进巧克力多少千克？当40千克花生用完时,奶粉还有多少千克？

答案：
(1)巧克力:$210×\frac{4}{4 + 2 + 1}=120$（千克）花生:$210×\frac{2}{4 + 2 + 1}=60$（千克） 奶粉:$210×\frac{1}{4 + 2 + 1}=30$（千克）
(2)巧克力:$40÷2×4 - 40 = 40$（千克） 奶粉:$40 - 40÷2×1 = 20$（千克）

3. (操作探究)把下面的梯形按$1:2:3$的面积比分成三部分。

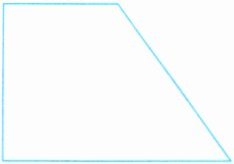
答案：
答案不唯一,如

4. 爸爸妈妈带明明去游乐场游玩,付了60元用于购票,找回5元。已知儿童票票价与成人票票价的比是$1:2$,则每张儿童票是多少元？每张成人票是多少元？

答案： $60 - 5 = 55$（元） 儿童票:$55×\frac{1}{1 + 2 + 2}=11$（元） 成人票:$55×\frac{2}{1 + 2 + 2}=22$（元）

5. (生活应用)笑笑家的后院有一块长方形菜地(一边靠墙),如果用篱笆把菜地围起来,靠墙的一边不围,那么共需要篱笆56米。如果菜地的长与宽的比是$3:2$,那么这块菜地的面积最大是多少平方米？

答案： 情况一，长边靠墙:用篱笆围的三条边的长度比是3:2:2 长:$56×\frac{3}{3 + 2 + A}=24$（米） 宽:$56×\frac{2}{3 + 2 + 2}=16$（米） 面积:$24×16 = 384$（平方米）情况二，宽边靠墙:用篱笆围的三条边的长度比是3:3:2 长:$56×\frac{3}{3 + 3 + 2}=21$（米） 宽:$56×\frac{2}{3 + 3 + 2}=14$（米） 面积:$21×14 = 294$（平方米） $294 ＜ 384$ 这块菜地的面积最大是384平方米

6. 周末,晓晓、丹丹、萱萱一共做了98个汤圆,晓晓比丹丹多做18个,丹丹和萱萱做的汤圆个数的比是$3:2$。晓晓做了(48)个汤圆,丹丹做了(30)个汤圆。

答案： 48 30 解析:丹丹和萱萱做の汤圆个数的比是3:2，可以把丹丹做の汤圆数量看成3份，萱萱就做了这样の2份，而“晓晓比丹丹多做18个”，晓晓做の可以看成比“3份”多18个。如果晓晓少做18个，那么她做の也是这样の3份，三人做の汤圆の总数就变成(98 - 18)个，用$(98 - 18)÷(3 + 3 + 2)$求出每份有10个汤圆，则丹丹做了$10×3 = 30$（个）汤圆，晓晓做了$30 + 18 = 48$（个）汤圆。

7. 有一批正方形砖,若用它们拼成一个长与宽之比为$5:4$的长方形,则余32块；若改拼成长与宽各增加1块正方形砖的大长方形,则少59块。这批正方形砖共有多少块？

答案：
$32 + 59 - 1 = 90$（块） $90×\frac{5}{4 + 5}=50$（块） $90 - 50 = 40$（块） $50×40 + 32 = 2032$（块）解析:如图,涂色部分一共铺了32 + 59 = 91(块)正方形砖，去掉右下角的这一块砖，剩下的90块砖就相当于空白长方形的长边、宽边一共铺的地砖数。把90块砖按5:4的比分配,分别求出空白长方形长边、宽边各铺的块数，然后求出空白长方形铺的总块数，再加上32，便是这批正方形砖的总块数。