第3页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
1. 求下面立体图形的表面积。
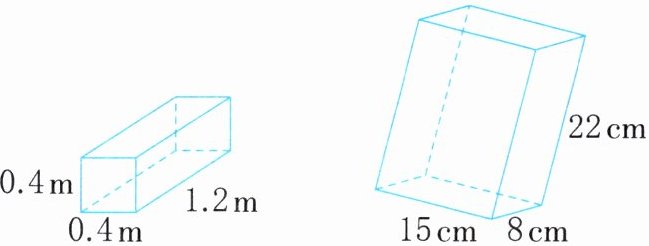

答案:
0.4×1.2×4+0.4×0.4×2=2.24(m²)(15×8+15×22+8×22)×2=1252(cm²)
(1)(南京玄武区)一个正方体的底面积是120平方分米,它的表面积是(
720
)平方分米。
答案:
解析:正方体的表面积是由它的6个面的面积之和构成的。因为正方体的每个面都是正方形,且面积都相等,所以只需将底面积乘以6即可得到表面积。
答案:
720平方分米。
答案:
720平方分米。
(2)一个长方体中相交于同一顶点的三个面的面积分别是16平方米、10平方米、40平方米,这个长方体的表面积是(
132
)平方米。
答案:
解析:
题目考查了长方体表面积的计算方法。
长方体有六个面,每个面都是一个矩形。
题目给出了相交于同一顶点的三个面的面积,这三个面分别是:前面(或后面)、左面(或右面)、上面(或下面)。
由于长方体的对面面积相等,所以可以得到:
前面和后面的面积都是16平方米;
左面和右面的面积都是10平方米;
上面和下面的面积都是40平方米。
长方体的表面积就是这六个面的面积之和。
因此,可以直接将这三个给定的面积乘以2(因为每个面积都有两个相对的面),然后将它们相加来得到长方体的表面积。
计算过程为:
表面积 $= 2 × (16+ 10 + 40) = 2 × 66 = 132$(平方米)。
答案:
132。
题目考查了长方体表面积的计算方法。
长方体有六个面,每个面都是一个矩形。
题目给出了相交于同一顶点的三个面的面积,这三个面分别是:前面(或后面)、左面(或右面)、上面(或下面)。
由于长方体的对面面积相等,所以可以得到:
前面和后面的面积都是16平方米;
左面和右面的面积都是10平方米;
上面和下面的面积都是40平方米。
长方体的表面积就是这六个面的面积之和。
因此,可以直接将这三个给定的面积乘以2(因为每个面积都有两个相对的面),然后将它们相加来得到长方体的表面积。
计算过程为:
表面积 $= 2 × (16+ 10 + 40) = 2 × 66 = 132$(平方米)。
答案:
132。
(3)萱萱用60厘米长的铁丝正好焊了一个正方体框架,给这个框架的表面糊纸,至少需要
150
平方厘米的纸。
答案:
解析:本题考查的知识点是正方体棱长和表面积的计算。
首先,正方体有12条棱,且每条棱的长度相等,由$正方体的棱长=铁丝总长÷12$,可得$正方体的棱长=60÷12=5(厘米)$。
然后,计算正方体一个面的面积,由$正方体一个面的面积=棱长×棱长$,可得$正方体一个面的面积=5×5=25(平方厘米)$。
最后,计算正方体的表面积,正方体有6个面,且面积都相等,由$正方体的表面积=正方体一个面的面积×6$,可得$正方体的表面积=25×6=150(平方厘米)$。
答案:150。
首先,正方体有12条棱,且每条棱的长度相等,由$正方体的棱长=铁丝总长÷12$,可得$正方体的棱长=60÷12=5(厘米)$。
然后,计算正方体一个面的面积,由$正方体一个面的面积=棱长×棱长$,可得$正方体一个面的面积=5×5=25(平方厘米)$。
最后,计算正方体的表面积,正方体有6个面,且面积都相等,由$正方体的表面积=正方体一个面的面积×6$,可得$正方体的表面积=25×6=150(平方厘米)$。
答案:150。
3.(生活应用)如图,轩轩网购了一套《百科全书》。
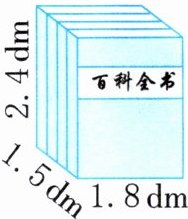
(1)有下图中三种尺寸的纸箱(从里面量,单位:dm),能装下这套书的纸箱有(
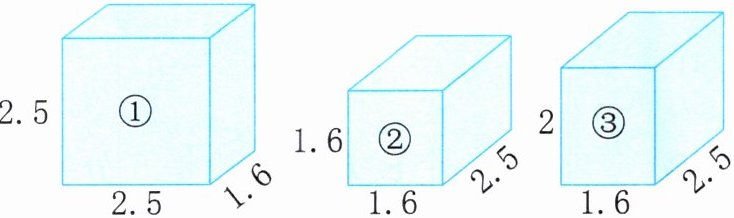
(2)在能装下这套书的纸箱中,哪种最节约纸板?制作一个这种纸箱,至少需要多少平方分米的纸板?

(1)有下图中三种尺寸的纸箱(从里面量,单位:dm),能装下这套书的纸箱有(
①③
)。
(2)在能装下这套书的纸箱中,哪种最节约纸板?制作一个这种纸箱,至少需要多少平方分米的纸板?
2<2.5 纸箱③最节约纸板 (2.5×1.6+2.5×2+1.6×2)×2=24.4(dm²)
答案:
(1)①③ (2)2<2.5 纸箱③最节约纸板 (2.5×1.6+2.5×2+1.6×2)×2=24.4(dm²)
4. 用三个棱长为a米的正方体拼成一个长方体,这个长方体的表面积比原来三个正方体的表面积之和减少了(
4a²
)平方米。
答案:
解析:本题考查的知识点是正方体和长方体表面积的计算及拼接变化。
三个独立的正方体总共有$3×6=18$个面,
当三个正方体拼接成一个长方体时,会减少4个面(因为两个正方体拼接会减少2个面,三个正方体拼接会减少4次面,但两两拼接共减少4个面),
每个面的面积是 $a^2$ 平方米,
所以,拼接后的长方体表面积比原来三个正方体的表面积之和减少的面积是4个面的面积,即 $4a^2$ 平方米,
答案:$4a^2$。
三个独立的正方体总共有$3×6=18$个面,
当三个正方体拼接成一个长方体时,会减少4个面(因为两个正方体拼接会减少2个面,三个正方体拼接会减少4次面,但两两拼接共减少4个面),
每个面的面积是 $a^2$ 平方米,
所以,拼接后的长方体表面积比原来三个正方体的表面积之和减少的面积是4个面的面积,即 $4a^2$ 平方米,
答案:$4a^2$。
5.(几何直观)体育课上,将一个垫子折叠成长方体(如图)。制作一个这样的垫子至少需要多少平方米的帆布?(接头处忽略不计)


答案:
5分米=0.5米 20厘米=0.2米 0.2÷2=0.1(米) (0.5×0.5+0.5×0.1+0.5×0.1)×2=0.7(平方米) 0.7×2=1.4(平方米) 解析:仔细观察可以发现,帆布的面积就是两个长是5分米、宽是5分米、高是(20÷2)厘米的长方体的表面积之和。
6. 用一根长120厘米的铁丝正好围成一个长15厘米、宽9厘米的长方体框架。如果在长方体框架的各个面都贴上彩纸,那么至少需要多少平方厘米的彩纸?
答案:
120÷4-15-9=6(厘米) (15×9+15×6+9×6)×2=558(平方厘米) 解析:先求出长方体框架的高,再求出长方体框架的表面积,即至少需要彩纸的面积。
7. ${}^{\star }$把一个表面积是150平方厘米的正方体切成两个完全相同的长方体,每个长方体的表面积是多少平方厘米?
答案:
(6+2)÷2=4(个) 150÷6×4=100(平方厘米) 解析:正方体的表面积是6个正方形的面积之和,把它切成两个完全相同的长方体,增加了2个面(正方形),这时两个长方体的表面积之和相当于正方体6+2=8(个)面的面积之和,因此每个长方体的表面积相当于正方体8÷2=4(个)面的面积之和。 方法归纳>> 厘清关系巧求长方体的表面积 解决此类问题时,不一定要求出长方体的长、宽、高,只要厘清每个长方体的表面积相当于原来正方体几个面的面积之和即可解题。
查看更多完整答案,请扫码查看


