第39页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
| | 糖/克 | 水/克 | 糖与糖水的质量比 |
| 甲杯 | 15 | 100 |
| 乙杯 | 20 | 120 |
| 丙杯 | 45 | 250 |
| 丁杯 | 30 | 180 |
(
| 甲杯 | 15 | 100 |
3:23
|| 乙杯 | 20 | 120 |
1:7
|| 丙杯 | 45 | 250 |
9:59
|| 丁杯 | 30 | 180 |
1:7
|(
丙
)杯的糖水最甜,(甲
)杯的糖水最淡,(乙
)杯和(丁
)杯的糖水同样甜。
答案:
(1)3:23 1:7 9:59 1:7 丙 甲 乙 丁
(2) (推理意识)$\frac {8}{25}= \frac {8+16}{25+
$\frac {48}{72}= \frac {48-
50
}$$\frac {48}{72}= \frac {48-
16
}{72-24}$
答案:
(2)50 16
六年级一班的男生人数是女生人数的1.5倍,男生人数和女生人数的比是
3:2
,女生人数和全班人数的比是2:5
。
答案:
(3)3:2 2:5
(4) 钟面上,时针的转速与分针的转速之比是(
1:12
)。
答案:
(4)1:12
(5) (生活应用)一根粗细均匀的蜡烛,第一次燃烧了它的$\frac {1}{7}$,第二次燃烧了剩下的$\frac {5}{6}$,这根蜡烛两次燃烧部分的比是
1:5
,已经燃烧的部分和剩余部分的比是6:1
。
答案:
(5)1:5 6:1
(6) 若从六年级一班调全班人数的$\frac {1}{7}$到六年级二班,则两班人数相等,原来六年级一班与六年级二班的人数比是(
7:5
)。
答案:
(6)7:5
2. (1) 若水果店里的香蕉占水果总质量的$\frac {1}{4}$,橘子占水果总质量的$\frac {2}{5}$,则水果店里香蕉和橘子的质量比是多少?
(2) 若水果店里香蕉质量的$\frac {1}{4}恰好与橘子质量的\frac {2}{5}$相等,则水果店里香蕉和橘子的质量比是多少?
(3) 若当水果店里的香蕉卖出$\frac {1}{4}$,橘子卖出$\frac {2}{5}$时,剩下的香蕉和橘子的质量相等,则水果店里香蕉和橘子原来的质量比是多少?
(2) 若水果店里香蕉质量的$\frac {1}{4}恰好与橘子质量的\frac {2}{5}$相等,则水果店里香蕉和橘子的质量比是多少?
(3) 若当水果店里的香蕉卖出$\frac {1}{4}$,橘子卖出$\frac {2}{5}$时,剩下的香蕉和橘子的质量相等,则水果店里香蕉和橘子原来的质量比是多少?
答案:
(1)$\frac{1}{4}:\frac{2}{5}=5:8$ (2)香蕉的质量×$\frac{1}{4}=$橘子的质量×$\frac{2}{5}$,则香蕉的质量:橘子的质量=$\frac{2}{5}:\frac{1}{4}=8:5$ (3)$1-\frac{1}{4}=\frac{3}{4}$ $1-\frac{2}{5}=\frac{3}{5}$ $\frac{3}{5}:\frac{3}{4}=4:5$ 解析:当水果店里的香蕉卖出$\frac{1}{4}$,橘子卖出$\frac{2}{5}$时,剩下的香蕉和橘子的质量相等,说明原来香蕉质量的$1-\frac{1}{4}=\frac{3}{4}$与原来橘子质量的$1-\frac{2}{5}=\frac{3}{5}$相等。这时本小题就转化成第
(2)小题的类型,再思考解答。
(2)小题的类型,再思考解答。
3. 两个相同的瓶子都装满了酒精溶液,一个瓶子中酒精与水的体积比是$3:1$,另一个瓶子中酒精与水的体积比是$4:1$。若把这两瓶酒精溶液混合,求混合液中酒精与水的体积比。
答案:
$(\frac{3}{1+3}+\frac{4}{1+4}):(\frac{1}{1+3}+\frac{1}{1+4})=31:9$ 解析:第一个瓶子中酒精的体积占酒精溶液体积的$\frac{3}{1+3}$,水的体积占酒精溶液体积的$\frac{1}{1+3}$;第二个瓶子中酒精的体积占酒精溶液体积的$\frac{4}{1+4}$,水的体积占酒精溶液体积的$\frac{1}{1+4}$。混合液中酒精与水的体积比为$(\frac{3}{1+3}+\frac{4}{1+4}):(\frac{1}{1+3}+\frac{1}{1+4})$,再化简即可。
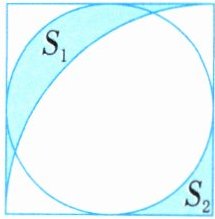
4. (探究创新)如下图,正方形的边长是2厘米,求涂色部分$S_{1}与S_{2}$面积的最简整数比。

答案:
3:1 解析:正方形的边长是2厘米,圆的面积=$3.14×(2÷2)^{2}=3.14$(平方厘米),最大扇形的面积=$\frac{1}{4}×3.14×2^{2}=3.14$(平方厘米),两者的面积相等,用正方形的面积分别减去这两部分的面积,剩下部分的面积也相等,即$S_{2}×4=S_{1}+S_{2}$,$S_{1}=S_{2}×3$,所以$S_{1}:S_{2}=3:1$。
查看更多完整答案,请扫码查看


