《2025年拔尖特训五年级数学上册人教版》

1.(1)计算下图的面积(单位:cm),小敏的算法是$(3+6)×8÷2-4×(6-3)÷2$。下面能表示小敏的思考过程的图是(③)。(填序号)


① ② ③ ④
(2)请你写出另外三幅图的算法。(只列算式)
① 8×3+(8−4)×(6−3)÷2
② 8×6−(4+8)×(6−3)÷2
③ 4×3+(3+6)×(8−4)÷2

答案：
(1)③　
(2)①8×3+(8−4)×(6−3)÷2
②8×6−(4+8)×(6−3)÷2
④4×3+(3+6)×(8−4)÷2

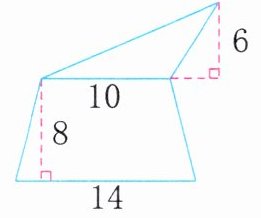
2. 求下面各组合图形的面积。(单位:cm)
(1)
(2)

答案：
(1)10×6÷2+(10+14)×8÷2=126(cm²)
(2)(8.5+14)×6.5÷2−8.5×3÷2=60.375(cm²)

3. 榫卯(sǔn mǎo),是一种在两个构件上采用凹凸部位相结合的连接方式,凸出的部分叫榫,凹进的部分叫卯。下图是一个卯结构的横截面,请算一算它的横截面面积。(单位:cm)

答案： (4×2+3+6)×5÷2=42.5(cm²)
(3+4)×2÷2=7(cm²)　42.5−7=35.5(cm²)
解析:大梯形的面积减去小梯形的面积即为卯结构的横截面面积。

4.(生活应用)下面是一块指示牌,其面积是多少平方米? 要在指示牌的正面刷油漆,每平方米需要油漆0.5千克,一共需要油漆多少千克?(单位:米)

答案： 0.4+0.1×2=0.6(米)　0.6×0.3÷2×2+1.2×0.4=0.66(平方米)　0.66×0.5=0.33(千克)
解析:观察题图可知，指示牌的面积=2个三角形的面积和+长方形的面积，三角形的底是2个0.1米与0.4米的和。

5. 如图,典典用一张长方形纸做手工,他将一角折叠,涂色部分的面积是多少平方厘米?

答案： (10+7)×6÷2−6×(10−7)÷2=42(cm²)
解析:涂色部分的面积=梯形的面积−空白三角形的面积,因为空白三角形是长方形纸的一个角折叠过来的,所以这也是一个直角三角形，一条直角边为长方形纸的宽,另一条直角边的长是10−7=3(cm)。

6.(思维过程)计算下图中涂色部分的面积。

答案：
5×4÷2+2×6÷2=16(cm²)
解析:如图，连接涂色四边形的对角线，将涂色四边形分成两个涂色三角形,涂色部分的面积即为两个涂色三角形的面积之和。