《2025年拔尖特训五年级数学上册人教版》

1.(1)用计算器计算下面各题,你发现了什么规律？



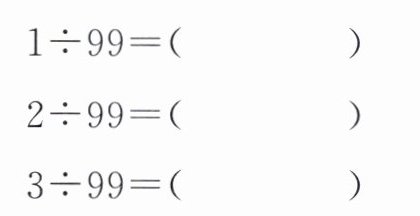
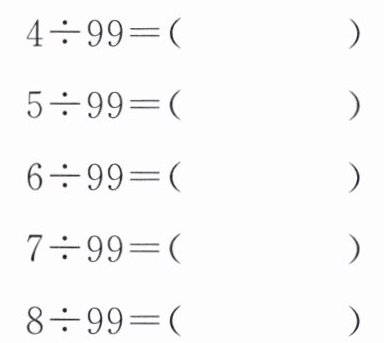
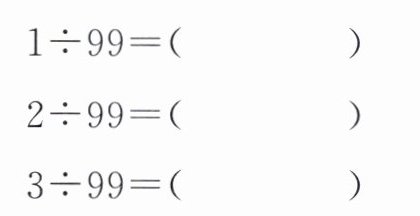
我发现：它们的商都是循环小数,并且除数不变,被除数乘几,商也就乘几。
(2)根据上面 3 道题的规律,直接写出下面各题的得数。

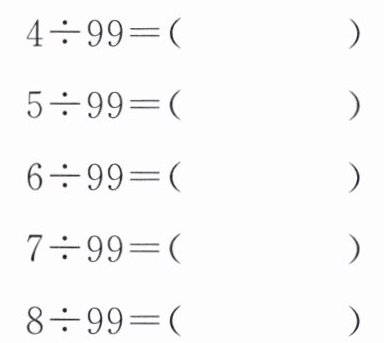
$0.\dot{0}\dot{4}$ $0.\dot{0}\dot{5}$ $0.\dot{0}\dot{6}$ $0.\dot{0}\dot{7}$ $0.\dot{0}\dot{8}$

答案： （1）$0.\dot{0}\dot{1}$ $0.\dot{0}\dot{2}$ $0.\dot{0}\dot{3}$ 循环 几
（2）$0.\dot{0}\dot{4}$ $0.\dot{0}\dot{5}$ $0.\dot{0}\dot{6}$ $0.\dot{0}\dot{7}$ $0.\dot{0}\dot{8}$

2.(推理意识)找规律填数。
11.11110411.11110311.111110211.11111101

答案： 11.111104 11.111103 11.1111102 11.11111101

$21\÷7= (3)$
$22.11\÷6.7= (3.3)$
$222.111\÷66.7= (3.33)$
$2222.1111\÷666.7= (3.333)$
$22222.11111\÷6666.7= (3.3333)$
$222222.111111\÷66666.7= (3.33333)$

答案： 3 3.3 3.33 3.333 3.3333 3.33333

4. 已知$1.99998\÷ A= 0.22222$,$2.99997\÷ A= 0.33333$,$3.99996\÷ A= 0.44444$,则$4.99995\÷ A= $0.55555；如果商是$0.77777$,那么算式为6.99993$÷ A$。

答案： 0.55555 6.99993
解析:通过观察可知,被除数的整数部分依次增加1,小数部分最后一个数依次减少1。商是五位小数,整数部分为0,小数部分的数字相同,这个数字=被除数整数部分的数字+1。

5.(操作探究)先用计算器计算下面各题,找一找规律,再写三个算式,并用计算器加以验证。
(1)$3\×0.5=$1.5
$3.3\×3.5=$11.55
$3.33\×33.5=$111.555
$3.333×333.5=1111.5555$ $3.3333×3333.5=11111.55555$ $3.33333×33333.5=111111.555555$(算式答案不唯一）
(2)$(10-1)\÷0.9=$10
$(200-2)\÷0.9=$220
$(3000-3)\÷0.9=$3330
$(40000-4)÷0.9=44440$ $(500000-5)÷0.9=555550$ $(6000000-6)÷0.9=6666660$(算式答案不唯一）

答案： （1）1.5 11.55 111.555 $3.333×333.5=1111.5555$ $3.3333×3333.5=11111.55555$ $3.33333×33333.5=111111.555555$(算式答案不唯一）解析:观察前面三个算式,发现第一个因数中有几个3,得数中就有几个1和几个5,小数点是1和5的分界线。根据这个规律再写三个算式即可。
（2）10 220 3330 $(40000-4)÷0.9=44440$ $(500000-5)÷0.9=555550$ $(6000000-6)÷0.9=6666660$(算式答案不唯一）解析:观察前三个算式,发现括号中被减数最高位上的数与被减数中0的个数和减数相同,括号外除数为0.9,商的个位上始终为0,位数等于括号中的被减数的位数,除个位外,其他数位上的数都与减数相同。根据这个规律再写三个算式即可。

6. ★观察下面的算式,总结规律,并解答问题。
$0.01+0.02= 0.03$
$0.04+0.05+0.06= 0.07+0.08$
$0.09+0.10+0.11+0.12= 0.13+0.14+0.15$
$0.16+0.17+0.18+0.19+0.20= 0.21+0.22+0.23+0.24$
……
如果按照上面的规律写下去,那么第 44 个算式的最后一个数是多少？

答案： 4.5×4.5-0.01=20.24
解析:观察每个算式的第一个数,可以发现第1个算式的第一个数是0.01,$0.01=0.1×0.1$;第2个算式的第一个数是0.04,$0.04=0.2×0.2$;第3个算式的第一个数是0.09,$0.09=0.3×0.3$……以此类推,第45个算式的第一个数是$4.5×4.5$,而第44个算式的最后一个数应比第45个算式的第一个数小0.01,所以第44个算式的最后一个数是$4.5×4.5-0.01=20.24$。